UNIT 5:

DISCRETE FOURIER

TRANSFORM

Summary

This unit introduces the Discrete Fourier Transform as a means for obtaining a frequency based representation of a digital signal. The special characteristics of the Fast Fourier Transform implementation are described.

When you have worked through this unit you should:

· be able to explain what information is represented on a magnitude spectrum and on a phase spectrum of a discrete signal

· be able to state the mathematical expression for the Discrete-time discrete-frequency Fourier Transform (DFT)

· understand how the direct implementation of the DFT operates

· appreciate that the direct implementation of the DFT is very inefficient, and that the Fast discrete-time discrete-frequency Fourier Transform (FFT) provides a more efficient means of its calculation

· have a qualitative understanding of the operation of the decimation-in-time form of the FFT

· be able to predict how simple sine and cosine signals appear on the DFT in the region from 0 to F_s.

Concepts

A digital signal of finite duration x[1..N] can be specified in the time domain as a sequence of N scaled impulses occurring at regular sampling instants: each impulse taking on the amplitude of the signal at that instant. The same signal may also be described as a combination of N complex sinusoidal components X[0..N-1], each of a given frequency and phase, and each being a harmonic of the sampling rate/N. This representation, called a frequency-domain representation, may be obtained from the time-domain form through the use of the Discrete Fourier Transform or DFT. The time domain form and the frequency domain form are simply different ways of representing the same digital signal, one is chosen over the other simply in terms of utility for a given purpose.

The Discrete Fourier Transform X(f) of a signal x[1..N] is defined as:

1

where X[k] is the amplitude of the kth harmonic, where k varies from 0 to N-1 and where k/N represents a fractional frequency value of the sampling rate. In general X[] and x[] can hold complex values, and X[] will be complex even if x[] is purely real.

The graph of |X(f)| against frequency is known as the magnitude spectrum. The graph of arg X(f) against frequency is known as the phase spectrum.

By copying a real digital signal into a complex sequence x[1..N], the DFT has a straightforward algorithmic implementation (shown in ComplexDFT()), using complex multiplication with the complex exponential defined as:

2

and hence:

3

We can also define the inverse transform, from the frequency representation X[] back to the time representation x[]:

4

where n varies from 1 to N. We have chosen to place the scaling factor 1/N in the forward transform, but many authorities place it in the inverse transform. We choose to place it here because it leads to harmonic amplitudes which are normalised to the sequence length, and hence independent of the amount of signal analysed. This leads naturally to an equivalence between the energy in the signal and the energy in the spectrum:

5

The frequency spectrum is often displayed in log magnitude terms in units of decibels (dB), and may be converted using:

6

From a real signal at a sampling rate F_s, the DFT provides N harmonic amplitudes at frequencies from 0 to . However the frequencies from 0 to F_s/2 are aliased to the region F_s/2 to F_s, so only the lower N/2 amplitudes are important.

The phase angles may be converted to degrees using:

7

The Fast Fourier Transform or FFT is simply a particular implementation of the DFT, that gives identical results, but which takes considerably less calculation. It does this by eliminating a great deal of redundant computation in the DFT in the circumstances when the sequence length N is a power of 2 (i.e. 4, 8, 16, 32, 64, etc).

In a normal DFT, each harmonic amplitude is the result of N complex multiplies with N different complex exponentials - giving a total of N² multiplies for all N harmonics. When N is a power of 2, many of these multiplies concern identical numerical multiplicands and many of the complex exponentials are zero or 1. When redundant computation is removed, the number of multiplies is Nlog₂(N) rather than N² and this represents a very large saving when N is large (e.g. for 1024 samples there is 100 times less calculation).

At the heart of the FFT is a simple algebraic manipulation that takes two input values, performs a multiply operation with a complex exponential and produces two output values. This basic unit is called a 'butterfly', and for two complex inputs a and b, a frequency W (=2πkn/N), and outputs p and q, the butterfly calculation is

8

We shall diagram this basic operation as:

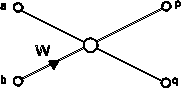1

This actually represents the DFT of a 2 sample waveform. Longer waveforms can be processed by combining these butterfly operations with variations on the value of W. Thus a DFT of an 8 sample waveform x[0] to x[7] can be graphed as:

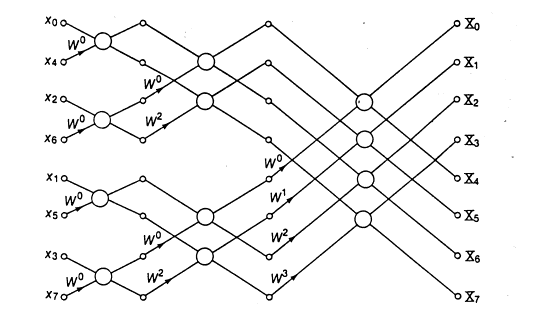
Where W^j is one of the frequencies in the DFT calculation (=2πj/N). This signal flow graph is the basis of the ComplexFFT() implementation. To operate the graph, the input signal is shuffled into the spectrum array in an order known as bit-reversed addressing. Then each column of butterfly operations is performed, so that the signal 'moves' left-to-right through the graph, turning into the DFT spectrum.

A more mathematical explanation of the FFT is also available.

Implementation Note

The FFT routines have not been written for maximum efficiency. Note that the calculation of the bit-reversed addresses and the values of the complex exponentials need only be performed once for a given size of transform. Since typical use of the FFT is the repeated use of the transform on constant lengths of waveform, these tables may be pre-calculated and stored.

Bibliography

Meade & Dillon, Signals and Systems, Chapter 7, pp130-144.

Lynn & Fuerst, Introductory Digital Signal Processing, Chapter 7.

Orfanidis, Introductory Signal Processing, Chapter 9.

Algorithms

Algorithm 5.1 Complex to Complex Discrete Fourier Transform

// cdft.cpp -- complex-to-complex Discrete Fourier Transform

//

// C++ (c) 1996 Mark Huckvale University College London

#include "tools.h"

#include "cdft.h"

// The ComplexDFT function implements a general complex to

// complex discrete fourier transform

Spectrum ComplexDFT(const ComplexWaveform& x)

{

Spectrum s(x.count(),x.count()/x.rate());

// for each output harmonic

for (int i=0;i<x.count();i++) {

// get frequency

double f = (2 * PI * i) / x.count();

// compute complex sum

Complex sum=0.0;

for (int j=0;j<x.count();j++)

sum += x[j+1] * exp(Complex(0.0,-f*j));

// scale

s[i] = sum/x.count();

}

return s;

}

// The ComplexIDFT function implements a general complex to

// complex inverse discrete fourier transform

ComplexWaveform ComplexIDFT(const Spectrum& s)

{

ComplexWaveform x(s.count(),s.count()/s.rate());

// for each output sample

for (int i=0;i<x.count();i++) {

// get frequency

double f = (2 * PI * i) / x.count();

// compute complex sum

Complex sum=0.0;

for (int j=0;j<x.count();j++)

sum += s[j] * exp(Complex(0.0,f*j));

x[i+1] = sum;

}

return x;

}

Algorithm 5.2 Complex Fast Fourier Transform

// cfft.cpp -- implementation of complex-to-complex Fast Fourier Transform

//

// C++ (c) 1996 Mark Huckvale University College London

#include "tools.h"

#include "cfft.h"

// The iLog2 function returns the integer log based 2

int iLog2(int x)

{

int p=0;

int y=1;

while (y < x) {

p++;

y *= 2;

}

return p;

}

// The iPow2 function returns the integer power of 2

int iPow2(int p)

{

int x=1;

while (p > 0) {

p--;

x *= 2;

}

return x;

}

// The FFTBitReverseTable function returns a dynamically-allocated

// table of indexes for FFT in-place sample shuffling

int * FFTBitReverseTable(int size)

{

int *idx = new int[size];

// find # bits involved

int nbit = iLog2(size);

// for each table entry

for (int i=0;i<size;i++) {

// store bit reversed index

int a1 = i;

int a2 = 0;

for (int j=1;j<=nbit;j++) {

a2 *= 2;

if (a1 & 1) a2 |= 1;

a1 /= 2;

}

idx[i] = a2;

}

return idx;

}

// The FFTButterfly function performs the key FFT cross-multiply

void FFTButterfly(Complex& upper,Complex& lower,const Complex& w)

{

Complex temp = lower * w;

lower = upper - temp;

upper = upper + temp;

}

// The ComplexFFT function implements a fast complex to

// complex discrete fourier transform

Spectrum ComplexFFT(const ComplexWaveform& x)

{

int size = iPow2(iLog2(x.count()));

Spectrum s(size,size/x.rate());

// get bit reverse table

int *amap = FFTBitReverseTable(size);

// shuffle input data into spectrum

for (int i = 0 ; i < size ; i++)

s[amap[i]] = x[i+1];

// uses bad index capability of x[]

// do multiple butterfy passes over data

// with steps of 1,2,4,..,N

for (int d = 1 ; d < size ; d *= 2) {

// for each start position

for (int j = 0 ; j < d ; j++) {

Complex w = exp(Complex(0,-(PI*j)/d));

// for each step

for (int i = j ; i < size ; i += 2*d)

// do butterfly

FFTButterfly(s[i],s[i+d],w);

}

}

// normalise

for (int i = 0 ; i < size ; i++)

s[i] /= x.count();

delete [] amap;

return s;

}

// The ComplexIFFT function implements a fast complex to

// complex inverse discrete fourier transform

ComplexWaveform ComplexIFFT(const Spectrum& s)

{

ComplexWaveform x(s.count(),s.count()/s.rate());

// get bit reverse table

int *amap = FFTBitReverseTable(x.count());

// shuffle input data into waveform

for (int i = 0 ; i < s.count() ; i++)

x[i+1] = s[amap[i]];

// do multiple butterfy passes over data

// with steps of 1,2,4,..,N

for (int d = 1 ; d < s.count() ; d *= 2) {

// for each start position

for (int j = 0 ; j < d ; j++) {

Complex w = exp(Complex(0,(PI*j)/d));

// for each step

for (int i = j+1 ; i <= s.count() ; i += 2*d)

// do butterfly

FFTButterfly(x[i],x[i+d],w);

}

}

delete [] amap;

return x;

}

Example Programs

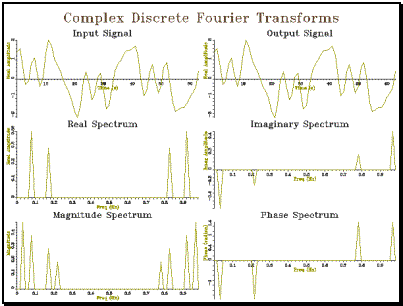
Example 5.1 Complex Discrete Fourier Transform

// cdft_cpp -- demonstration of Complex DFT & IDFT

#include "tools.h"

#include "cdft.h"

const int SIZE=64;

int main()

{

int i;

// create a test signal

ComplexWaveform ip(SIZE,1);

for (i=1;i<=SIZE;i++) {

double f = 2 * PI * (i-1) / SIZE;

ip[i] = Complex(1.0 * sin( 2*f) +

0.8 * cos( 5*f) +

0.6 * cos(11*f) +

0.4 * sin(14*f),

0);

}

// generate spectrum

Spectrum s=ComplexDFT(ip);

// generate signal again

ComplexWaveform op=ComplexIDFT(s);

// plot as graphs

Graph gr(3,2,"Complex Discrete Fourier Transforms");

ip.plotReal(gr,1,"Input Signal");

op.plotReal(gr,2,"Output Signal");

s.plotReal(gr,3,"Real Spectrum");

s.plotImag(gr,4,"Imaginary Spectrum");

s.plotMag(gr,5,"Magnitude Spectrum");

s.plotPhase(gr,6,"Phase Spectrum");

gr.close();

}

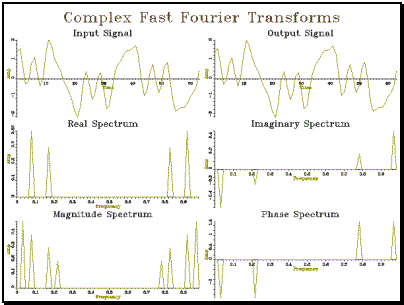
Example 5.2 Complex Fast Fourier Transform

// cfft_cpp -- demonstration of Complex FFT & IFFT

#include <iostream.h>

#include "tools.h"

#include "cfft.h"

const int SIZE=64;

int main()

{

int i;

// create a test signal

ComplexWaveform ip(SIZE,1);

for (i=1;i<=SIZE;i++) {

double f = 2 * PI * (i-1) / SIZE;

ip[i] = Complex(1.0 * sin( 2*f) +

0.8 * cos( 5*f) +

0.6 * cos(11*f) +

0.4 * sin(14*f),

0);

}

// generate spectrum

Spectrum s=ComplexFFT(ip);

// generate signal again

ComplexWaveform op=ComplexIFFT(s);

// plot as graphs

Graph gr(3,2,"Complex Fast Fourier Transforms");

ip.plotReal(gr,1,"Input Signal","Time","Amp");

op.plotReal(gr,2,"Output Signal","Time","Amp");

s.plotReal(gr,3,"Real Spectrum","Frequency","Amp");

s.plotImag(gr,4,"Imaginary Spectrum","Frequency","Amp");

s.plotMag(gr,5,"Magnitude Spectrum","Frequency","Amp");

s.plotPhase(gr,6,"Phase Spectrum","Frequency","Amp");

gr.close();

}

Exercises

5.1 The inverse DFT provides a simpler method to synthesize a square wave: set up the spectrum of a square wave and call ComplexIDFT(). Set up a spectrum as follows:

Spectrum(1000,0.05); // 0..19,980Hz in 1000 steps

Then put in the odd harmonics of 100Hz with appropriate amplitudes (amplitude of nth harmonic is just 1/n). That is, put in amplitudes of 1.0 at spectrum position 5, 0.33 at position 15, 0.2 at position 25, etc. Don’t forget to put in the mirror images at positions 995, 985, 975, etc. Plot your spectrum and the result of the inverse DFT.

How would you change your solution to use an FFT? Why might you want to?

5.2 Modify Examples 5.1 and 5.2 to explore the differences between an exact DFT of a 40 point test waveform and the FFT of the same waveform suffixed with 24 zeros. Plot a graph showing the magnitude spectrum and the phase spectrum of the same signal analysed in these two ways.

What differences are there between an FFT of a 64 point waveform and an FFT of the same waveform appended with 64 zeros?