UNIT
7:
DIGITAL
FILTER
DESIGN
Summary
This
unit is concerned primarily with the design of digital systems having frequency
response characteristics appropriate to low-pass, high-pass and band-pass
filters. It is concerned with both
non-recursive and recursive designs: the former based on the Fourier transform
method, the second through the so-called ‘bilinear’ transformation of analogue
designs.
When you have worked through this unit you should:
· be able to explain how
simple non-recursive filters may be designed by the DFT method
· understand how low-pass
non-recursive filters may be transformed into high-pass and band-pass designs
· understand how the Kaiser
window provides a means for building a simple non-recursive filter from
specifications of the stop-band ripple and the width of the transition region.
· be able to explain how
simple recursive filters may be designed through the use of the Butterworth
formulae
· understand how the use of
cascaded second-order sections provides a means for implementing Butterworth
filters from the pole-zero diagram
· understand how recursive
low-pass filters may be transformed into high-pass and band-pass designs.
· be able to discuss the
relative merits of recursive and non-recursive designs for different
applications.
Concepts
Non-recursive Filter Design
We
seek to find a set of a[] (numerator) coefficients for a linear time-invariant
system that would implement a low-pass filter: that is the impulse response of
a low-pass non-recursive filter. We
then consider how to transform these
coefficients into high-pass or band-pass forms.
We
first note that the Fourier transform of a rectangular window has a
characteristic shape known as a sin(x)/x
or sinc(x) function. Thus for an ideal low-pass filter response,
which has a rectangular shape, the related impulse response must follow this
sin(x)/x shape. Since the response of a
digital system repeats periodically with frequency (once per sampling
frequency), we can choose to consider a rectangular filter within a response
that extends from -sample-rate/2 to +sample-rate/2, and this will give us an
impulse response that is also symmetric about t=0:
|
|
For a cut-off angular frequency of wc the
formula for this impulse response is just:
![]()
where wc = 2pfc, where fc = fraction of
sampling rate, and where n extends over all positive and negative times.
To
generate an impulse response of a certain maximum size, it is best to window
the resulting coefficients, rather than simply truncate them. This can be easily performed with a Hamming
window. We may then shift the filter
coefficients in time to get a causal filter.
See NRLowPass().
To
obtain the impulse response of a high-pass or band-pass filter, we note that
all we need do is shift the frequency response curve along the frequency axis -
so the rectangular response is now either symmetric about the half-sample-rate
frequency - in which case we get a high-pass filter, or is now over a block of
frequencies - in which case we get a band-pass filter. The process of shifting the response in the
frequency domain is a process of convolution with another response which
consists solely of an impulse at the new centre frequency of the block, that is
the spectrum of a signal having a single frequency component at the new centre
frequency, that is the spectrum of a sinusoidal signal. This convolution in the frequency domain
manifests itself in the time domain by a multiplication of the impulse response
by a cosine wave of the appropriate frequency.
So to shift the impulse response of a low-pass filter up to a new centre
angular frequency w, we generate:
![]()
For
the special case that the new rate is half the sample rate (i.e. when w=p) the modulation consists of multiplying h[] by +1,
-1, +1, -1, .... See the
implementations of NRHighPass() and NRBandPass() to exemplify this.
While
the Hamming window is a simple and useful method for truncating the impulse
response, it is rather inflexible. The
Hamming window gives us a flat pass band and fairly good attenuation in the
stop band, but at the expense of a fairly broad transition band. Sometimes we wouldn't mind more ripple in
the pass band if that allowed us to have a narrower transition region. We can achieve this by designing a windowing
function with the appropriate properties and use that to truncate the sinc
function impulse response. A simple way
to achieve this is with the parametric Kaiser
window.
The
Kaiser window is defined as:
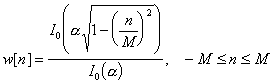
Where
I0 is the zeroth order modified Bessel function of the first kind,
which has a complex mathematical description, but a straightforward algorithmic
description shown in Algorithm 7.2. The
parameter a controls the tradeoff
between transition width and ripple. We
can give a heuristic for the selection of a and M from a specification of (i) the allowed stop band ripple A expressed as decibels below the
passband, and (ii) the transition width D expressed as a fraction
of the sample rate:
if A >= 50, then a =
0.1102(A - 8.7)
if 21 < A < 50, then a =
0.5842(A - 21)0.4 + 0.07886(A - 21)
if A <= 21, then a = 0
Where
the ripple level is less than 21dB from the pass band, then we end up with a
rectangular window. M, the half-size of the window is then
given by:
![]()
Algorithm
7.2, Kaiser designs a window according to these formulae, which could be used
to substitute for the Hamming window used in NRLowPass, etc.
Recursive Filter Design
The
design of recursive filters is considerably more complex than the design of
non-recursive filters. The design task
is to place poles and zeros on the complex plane, such that the frequency
response has the desired characteristics.
This can either be performed through experience or with an interactive
design tool. We choose to look at the
design formulae developed for analogue filters: specifically for Butterworth
designs. These can then be transformed
into the digital domain through the use of an algebraic transformation that
maps the analogue frequencies 0..¥ into the periodically
repeating angular frequencies 0..2p. The mechanism used is called the bilinear transformation.
A digital Butterworth low-pass filter of order n has n poles arranged on a circular arc
on the complex plane and n zeros located at z = (-1,0). If n
is even, the poles form n/2 conjugate
pairs. If n is odd, then a pole on the real axis is added. If we keep to even n for convenience the location of the poles are given by the
formulae:
![]()
where
the real and imaginary parts are given by:
![]()
![]()
and where
![]()
For
simplicity of implementation, the routine ButterworthPoles() calculates the positions
of n/2 poles on the positive imaginary axis, and each pole-pair is then used to
implement a separate linear system (a second-order
section) in the routine ButterworthLowPass(). The resulting chain of linear systems is returned for
filtering operation.
The
transformation of the low-pass design into high-pass is straightforward: it
simply involves reflecting the poles and zeros around the imaginary axis. See ButterworthHighPass().
The
transformation of the low-pass design into band-pass is more complex and involves
a doubling of the filter order and a rotation of the poles around the unit
circle. For a band-pass filter
extending from angular frequencies wl to wh, we first
calculate the poles and zeros for a low pass filter with a cut-off frequency wc
= (wh‑wl)/2.
Then each pole or zero at z is
moved to a new location by the formula:
![]()
where
A is given by:
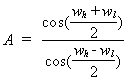
See ButterworthBandPass().
A
Butterworth design gives us a filter with a maximally-flat passband and good
stop-band attenuation, so that it makes a good general purpose filter. As before, however, other designs can give
us a narrower transition region at the cost of greater ripples in the pass-
and/or stop-bands. Many DSP packages
give design programs for Chebyshev and Elliptic filter designs, but their
essential operation is the same as the Butterworth design.
Algorithms
Algorithm 7.1 Non-recursive filter design
|
// nonrec.cpp -- non-recursive filter design // // C++ (c) 1996 Mark Huckvale University College London // NRLowPass() build NR low-pass filter // NRHighPass() build NR high-pass filter // NRBandPass() build NR band-pass filter #include "tools.h" #include "ltisys.h" // sinc() or sin(x)/x function double sinc(double x) { if (x==0) return cos(x); else return sin(x)/x; } // Create non-recursive low-pass filter by Fourier Transform method LTISystem NRLowPass( double freq, // corner freq (fraction of sampling rate) int ncoeff // # coefficients ) // returns LTI system to specification { int i; // convert frequency double omega = 2 * PI * freq; // build half-sized window from sinc function int nhalf = ncoeff/2; Waveform hwv(nhalf,1.0); for (i=1;i<=nhalf;i++) hwv[i] = omega * sinc(i*omega)/PI; // window with (half-)hamming window for (i=1;i<=nhalf;i++) hwv[i] *= 0.54 + 0.46 * cos(i*PI/nhalf); // create new LTI System LTISystem lpfilt(2*nhalf,0); // copy impulse response into system // (indexed -nhalf .. 0 .. nhalf) lpfilt.a[nhalf] = omega/PI; for (i=1;i<=nhalf;i++) { lpfilt.a[nhalf-i] = hwv[i]; lpfilt.a[nhalf+i] = hwv[i]; } return lpfilt; } |
|
// create high-pass non-recursive filter from low-pass prototype LTISystem NRHighPass( double freq, // corner freq (fraction of sampling rate) int ncoeff // # coefficients ) // returns LTI system { // get low-pass version LTISystem hpfilt = NRLowPass(0.5-freq,ncoeff); // now modulate with cos(n*PI) = +1,-1,+1,-1,... int nhalf = hpfilt.a.count()/2; for (int i=1;i<=nhalf;i+=2) { hpfilt.a[nhalf-i] = -hpfilt.a[nhalf-i]; hpfilt.a[nhalf+i] = -hpfilt.a[nhalf+i]; } return hpfilt; } // create band-pass non-recursive filter from low-pass prototype LTISystem NRBandPass( double lofreq, // low corner freq (fraction of sampling rate) double hifreq, // high corner freq (fraction of sampling rate) } int ncoeff // # coefficients ) // returns LTI system { // get low-pass prototype LTISystem bpfilt = NRLowPass((hifreq-lofreq)/2,ncoeff); // now modulate with cos(n*centrefreq) int nhalf = bpfilt.a.count()/2; double cf = 2*PI*(lofreq+hifreq)/2; bpfilt.a[nhalf] = 2 * bpfilt.a[nhalf]; for (int i=1;i<=nhalf;i++) { bpfilt.a[nhalf-i] = 2 * bpfilt.a[nhalf-i] * cos(i*cf); bpfilt.a[nhalf+i] = 2 * bpfilt.a[nhalf+i] * cos(i*cf); } return bpfilt; } |
Algorithm 7.2 - Kaiser Window
|
// kaiser.cpp - Kaiser window design // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include “kaiser.h” // zeroth order modified Bessel function of the first kind const int ITERLIMIT=15; const double CONVERGE=1.0E-8; double besselI0(double p) { // initialise iterative loop p = p/2; double n = 1, t = 1, d = 1; // iteration int k = 1; double v; do { n = n * p; d = d * k; v = n / d; t = t + v * v; } while ((++k < ITERLIMIT) && (v > CONVERGE)); return t; } // return half-Kaiser window to specification Waveform Kaiser( double ripple, // input stop-band ripple (dB) double twidth, // input transition width // (fraction of sample rate) int kmaxlen) // maximum window size { double alpha; // window coefficient int hlen; // half window length // set Kaiser window coefficient (design rule) if (ripple <= 21) alpha = 0; else if (ripple < 50) alpha = 0.5842*exp(0.4*log(ripple-21))+0.07886*(ripple-21); else alpha = 0.1102*(ripple - 8.7); // set Kaiser window size (design rule) if (ripple < 7.95) hlen = 0; else hlen = 1+(int)((ripple - 7.95)/(28.72*twidth)); if ((hlen+1) > kmaxlen) hlen = kmaxlen - 1; // build window Waveform kwin(hlen+1,1.0); // output window // calculate window 1..hlen+1 double d = besselI0(alpha); kwin[1] = 1.0; for (int n=1;n<=hlen;n++) { double v = n/(double)hlen; kwin[n+1] = besselI0(alpha*sqrt(1-v*v))/d; } return kwin; } |
Algorithm 7.3 Butterworth Recursive Filter Design
|
// ltisysch.h -- LTI System Chain class declaration // // C++ (c) 1996 Mark Huckvale University College London #ifndef _LTISysCh_H #define _LTISysCh_H #include "ltisys.h" class LTISystemChain { public: // public for demonstration purposes LTISystem *section; // array of sections int nsection; // # sections public: // constructors LTISystemChain(int n=1); LTISystemChain(const LTISystemChain& lch); ~LTISystemChain(); // assignment LTISystemChain& operator= (const LTISystemChain& lch); LTISystem& operator[] (int idx); // clear system void clear(); // run system double operator() (double ival); // frequency response Complex response(double freq) const; }; #endif |
|
// butter.cpp -- Butterworth filter design // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "ltisys.h" #include "ltisysch.h" #include "butter.h" // ButterworthPoles() calculate positions of z-plane // poles to Butterworth formula // ButterworthLowPass() build low-pass recursive filter // to Butterworth design // ButterworthHighPass() build high-pass recursive filter // ButterworthBandPass() build band-pass recursive filter // position nsection poles for Butterworth Low-pass ComplexWaveform ButterworthPoles( double freq, // cut-off frequency (fraction) int nsection // number of 2nd order sections reqd ) // returns array of pole positions // on positive imaginary axis only { // get array of complex values ComplexWaveform poles(nsection,1); // calculate angles double w = PI * freq; double tanw = sin(w)/cos(w); // calculate +im pole position for each section for (int m=nsection;m<=2*nsection;m++) { // Butterworth formula adapted to z-plane double ang = (2*m + 1) * PI / (4*nsection); double d = 1 - 2*tanw*cos(ang) + tanw*tanw; poles[m-nsection+1] = Complex((1 - tanw*tanw)/d, 2 * tanw * sin(ang)/d); } return poles; } |
|
// build Butterworth low-pass filter LTISystemChain ButterworthLowPass( double freq, // cut-off frequency (fraction) int nsection // number of 2nd order sections reqd ) // returns array of LTI systems { // create empty system chain LTISystemChain lpfilt(nsection); // get pole positions ComplexWaveform pol = ButterworthPoles(freq,nsection); // convert each conjugate pole pair to // difference equation for (int i=0;i<nsection;i++) { lpfilt[i] = LTISystem(2,2); // put in conjugate pole pair lpfilt[i].b[1] = -2.0 * pol[i+1].real(); lpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() + pol[i+1].imag() * pol[i+1].imag(); // put 2 zeros at (-1,0) double tot = 4.0/(1 + lpfilt[i].b[1] + lpfilt[i].b[2]); lpfilt[i].a[0] = 1.0/tot; lpfilt[i].a[1] = 2.0/tot; lpfilt[i].a[2] = 1.0/tot; } return lpfilt; } // build Butterworth high-pass filter LTISystemChain ButterworthHighPass( double freq, // cut-off frequency (fraction) int nsection // number of 2nd order sections reqd ) // returns array of LTI systems } { // create empty system chain LTISystemChain hpfilt(nsection); // get pole positions for low-pass ComplexWaveform pol = ButterworthPoles(0.5-freq,nsection); // flip all the poles over to get high pass for (int i=1;i<=nsection;i++) pol[i] = Complex(-pol[i].real(),pol[i].imag());
// convert each conjugate pole pair to // difference equation for (int i=0;i<nsection;i++) { hpfilt[i] = LTISystem(2,2); // put in conjugate pole pair hpfilt[i].b[1] = -2.0 * pol[i+1].real(); hpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() + pol[i+1].imag() * pol[i+1].imag(); // put 2 zeros at (1,0) hpfilt[i].a[0] = 1.0; hpfilt[i].a[1] = -2.0; hpfilt[i].a[2] = 1.0; // normalise to unity gain double gain = mag(hpfilt[i].response(0.5)); hpfilt[i].a[0] = hpfilt[i].a[0]/gain; hpfilt[i].a[1] = hpfilt[i].a[1]/gain; hpfilt[i].a[2] = hpfilt[i].a[2]/gain; } return hpfilt; } |
|
// build Butterworth band-pass filter LTISystemChain ButterworthBandPass( double lofreq, // low cut-off frequency (fraction) double hifreq, // high cut-off frequency (fraction) int nsection // number of 2nd order sections reqd ) // returns array of LTI systems { // force even # sections if ((nsection%2)==1) nsection++; // create empty system chain LTISystemChain bpfilt(nsection); // get pole positions for low-pass of equivalent width ComplexWaveform pol = ButterworthPoles(hifreq-lofreq,nsection/2); // translate the poles to band-pass position ComplexWaveform bpol(nsection,1); double wlo = 2*PI*lofreq; double whi = 2*PI*hifreq; double ang = cos((whi+wlo)/2)/cos((whi-wlo)/2); for (int i=1;i<=nsection/2;i++) { Complex p1 = Complex(pol[i].real()+1,pol[i].imag()); Complex tmp = sqrt(p1*p1*ang*ang*0.25-pol[i]); bpol[2*i-1] = (p1*ang*0.5) + tmp; bpol[2*i] = (p1*ang*0.5) - tmp; } // convert each conjugate pole pair to // difference equation for (int i=0;i<nsection;i++) { bpfilt[i] = LTISystem(2,2); // put in conjugate pole pair bpfilt[i].b[1] = -2.0 * pol[i+1].real(); bpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() + pol[i+1].imag() * pol[i+1].imag(); // put zeros at (1,0) and (-1,0) bpfilt[i].a[0] = 1.0; bpfilt[i].a[1] = 0.0; bpfilt[i].a[2] = -1.0; // normalise to unity gain double gain = mag(bpfilt[i].response((hifreq+lofreq)/2)); bpfilt[i].a[0] = bpfilt[i].a[0]/gain; bpfilt[i].a[1] = bpfilt[i].a[1]/gain; bpfilt[i].a[2] = bpfilt[i].a[2]/gain; } return bpfilt; } |
Bibliography
Lynn & Fuerst, Introductory Digital Signal
Processing, Chapter 5.
Orfanidis, Introduction to Signal
Processing, Chapters 10 & 11.
Example Programs
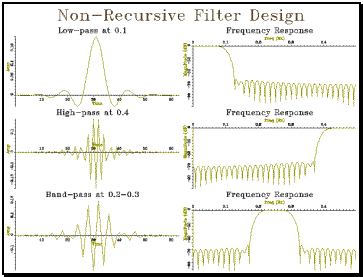
Example 7.1 Non-recursive filter
design
|
// nonrec_t.spc -- test program for non-recursive filter design #include "tools.h" #include "ltisys.h" #include "nonrec.h" int main() { Graph gr(3,2,"Non-Recursive Filter Design"); // calculate low-pass filter and plot LTISystem lp = NRLowPass(0.1,63); lp.a.plot(gr,1,"Low-pass at 0.1","Samples","Amp"); // calculate frequency response and plot Spectrum lpf(500,1000); for (int i=0;i<500;i++) lpf[i] = lp.response(i/1000.0); lpf.plotLogMag(gr,2,"Frequency Response"); // calculate high-pass filter and plot LTISystem hp = NRHighPass(0.4,63); hp.a.plot(gr,3,"High-pass at 0.4","Samples","Amp"); // calculate frequency response and plot Spectrum hpf(500,1000); for (int i=0;i<500;i++) hpf[i] = hp.response(i/1000.0); hpf.plotLogMag(gr,4,"Frequency Response"); // calculate band-pass filter and plot LTISystem bp = NRBandPass(0.2,0.3,63); bp.a.plot(gr,5,"Band-pass at 0.2-0.3","Samples","Amp"); // calculate frequency response and plot Spectrum bpf(500,1000); for (int i=0;i<500;i++) bpf[i] = bp.response(i/1000.0); bpf.plotLogMag(gr,6,"Frequency Response");
gr.close(); } |
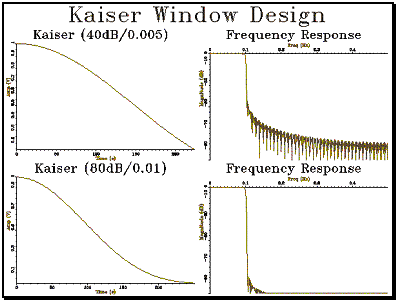
Example
7.2 - Demonstrate Kaiser Window
|
// kaiser_t.cpp -- test program for Kaiser window design #include "tools.h" #include "ltisys.h" #include "nonrec.h" #include "kaiser.h" const int MAXKAISERWIN=256; // maximum window length // Create non-recursive low-pass filter using Kaiser window LTISystem KaiserLowPass( double freq, // corner freq // (fraction of sampling rate) double ripple, // allowed ripple (dB) double twidth // transition width // (fraction of sampling rate) } ) // returns LTI System { int i; // get (half-)Kaiser window Waveform kwin = Kaiser(ripple,twidth,MAXKAISERWIN); int nhalf = kwin.count()-1; // generate one half of coefficients from // windowed sinc() function double omega = 2*PI*freq; for (i=0;i<=nhalf;i++) kwin[i+1] *= omega*sinc(i*omega)/PI; // copy into LTI System LTISystem lpfilt(2*nhalf,0); lpfilt.a[nhalf] = kwin[1]; for (i=1;i<=nhalf;i++) { lpfilt.a[nhalf-i] = kwin[i+1]; lpfilt.a[nhalf+i] = kwin[i+1]; } return lpfilt; } |
|
int main() { int i; // initialise graphics Graph gr (2,2,"Kaiser Window Design"); // plot Kaiser window 1 Waveform kwv1 = Kaiser(40.0,0.005,MAXKAISERWIN); kwv1.plot(gr,1,"Kaiser (40dB/0.005)"); // calculate and plot frequency response LTISystem lp1 = KaiserLowPass(0.1,40.0,0.005); Spectrum lpf1(500,1000); for (i=0;i<500;i++) lpf1[i] = lp1.response(i/1000.0); lpf1.plotLogMag(gr,2,"Frequency Response"); // plot Kaiser window 2 Waveform kwv2 = Kaiser(80.0,0.01,MAXKAISERWIN); kwv2.plot(gr,3,"Kaiser (80dB/0.01)"); // calculate and plot frequency response LTISystem lp2 = KaiserLowPass(0.1,80.0,0.01); Spectrum lpf2(500,1000); for (i=0;i<500;i++) lpf2[i] = lp2.response(i/1000.0); lpf2.plotLogMag(gr,4,"Frequency Response"); gr.close(); } |
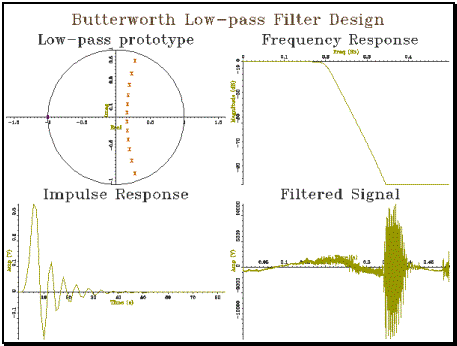
Example 7.3 Recursive filter design
|
// butter_t.cpp - test program for butterworth filter design #include "tools.h" #include "butter.h" #include "zplane.h" const double ILIMIT=1.0E-5; // length limit for impulse response const char *FILENAME="/app/sfs/demo/demo.sfs"; const char *SPITEM="sp."; const double SAMPLE=0.5; int main() { double fc; int ns; cout << "Enter cut-off freq (fraction of sampling rate) : "; cin >> fc; cout << "Enter # second order sections : "; cin >> ns; // initialise graphics Graph gr(2,2,"Butterworth Low-pass Filter Design"); // get poles and plot them ComplexWaveform pol = ButterworthPoles(fc,ns); ComplexWaveform poles = pol + pol; for (int i=pol.count()+1;i<=poles.count();i++) poles[i] = Complex(poles[i].real(),-poles[i].imag()); ComplexWaveform zeros(1,1); zeros[1] = Complex(-1,0); PlotZPlane(poles,zeros,gr,1,"Low-pass prototype"); // build chain of second order sections LTISystemChain lpfilt = ButterworthLowPass(fc,ns); // calculate frequency response Spectrum lpfr(500,1000); for (int i=0;i<500;i++) lpfr[i] = lpfilt.response(i/1000.0); lpfr.plotLogMag(gr,2,"Frequency Response"); // measure and plot impulse response Waveform lpir(0,1); double lval = 0; // last output double oval = lpfilt(1.0); // put in unit pulse while ((fabs(oval) > ILIMIT) || (fabs(oval-lval) > ILIMIT)) { lpir += oval; // append sample lval = oval; // remember sample oval = lpfilt(0.0); // get next sample } lpir.plot(gr,3,"Impulse Response"); // plot some filtered speech Signal isig(1,1.0); isig.load(FILENAME,SPITEM,0.0,SAMPLE); Waveform fwv(isig.count(),isig.rate()); lpfilt.clear(); for (int i=1;i<=isig.count();i++) fwv[i] = lpfilt(isig[i-1]); fwv.plot(gr,4,"Filtered Signal"); gr.close(); } |
Exercises
7.1. Implement a band-pass filter that emulates
the telephone system, using a non-recursive filter with 32 coefficients with a
response extending from 300Hz to 3500Hz.
Use it to filter and display the speech signal
/app/sfs/demo/speech.sfs along with some representative spectra and a
frequency response curve.
7.2. Adapt the program from exercise 7.1 to use
a recursive filter with 2 second-order sections. Find methods for timing the execution speed of programs and
compare the efficiency of this program to the original (you may need to comment
out the display part for timing).