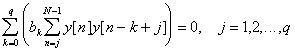UNIT 8:
LINEAR PREDICTION
Summary
Linear
prediction is a method for signal source modelling dominant in speech signal
processing and having wide application in other areas. Starting with a demonstration of the relationship
between linear prediction and the general difference equation for linear
systems, the unit shows how the linear prediction equations are formulated and
solved. The unit then discusses the use
of linear prediction for modelling the source of a signal and the signal
spectrum.
When
you have worked through this unit you should:
·
understand how
linear prediction can provide a model of a signal source
·
be able to state
the operational limitations of the modelling
·
understand in
qualitative terms how the equations are solved on a computer system
·
know how and when
to use linear prediction as an alternative to spectral analysis by the Fourier
transform
Concepts
Nature of linear prediction
The
object of linear prediction is to form a model of a linear time-invariant
digital system through observation of input and output sequences. That is: to estimate a set of coefficients
which will describe the behaviour of an LTI system when its design is not
available to us and we cannot choose what input to present.
Specifically,
linear prediction calculates a set of coefficients which provide an estimate -
or a prediction - for a forthcoming
output sample y'[n] given knowledge of previous input (x[]) and/or output (y[])
samples:
|
|
Where
a and b are called predictor
coefficients. It is immediately
clear that this estimate of the next output sample given the predictor
coefficients and previous input and output samples is directly related to the
general system difference equation we met in Unit 4. Even though we might not know the order of some LTI system, such
an estimator is an inherently sensible way to model its properties.
The
commonest form of linear prediction used in signal processing is one in which
the a coefficients are zero, so that
the output estimate is made entirely on the basis of previous output samples:
|
|
This
is called an all-pole model, which
may be seen by analogy with the frequency response equations of LTI
systems. The use of an all pole model
is motivated by a number of reasons:
(i) we often do not have access to the
input sequence,
(ii) many simple signal sources are
faithfully modelled by an all-pole model,
(iii) the all-pole model gives a system of
equations which may be efficiently solved.
The
relation of the linear predictor equation with the LTI system equation may be
more readily understood by introducing a predictor
error signal e[n], defined as the difference between the real output and
the prediction:
|
|
Hence we may write:
|
|
giving us a formulation in which the error signal takes the role of the
excitation signal, and the predictor coefficients define the filter.
Solution of linear
prediction equations
To estimate the predictor coefficients bk we first observe the behaviour of the system over N
samples, and set the order q of the
predictor required (usually N is much greater than q). We calculate the predictor coefficients by
finding values which minimise the energy in the error signal over the N samples[1]. This is called a least-squares minimisation, and leads to a system of q equations in q unknowns which may be solved to find the best fitting predictor
coefficients:
|
|
Where b0 is taken to be 1.
There are a number of methods for finding the solution to this system of
linear equations. The formulation above
is sometimes known as the covariance
formulation and is appropriate when estimating coefficients from a sample of a
non-stationary signal. If instead we
assume that the signal is zero outside the N sample region, we can find a
simpler formulation:
|
|
This is called the autocorrelation
formulation, since it contains components equivalent to the autocorrelation
coefficient ri defined as:
|
|
The autocorrelation formulation of the least squares fit of the predictor
coefficients produces a system of linear equations which can be represented in
matrix form and solved using standard methods such as Gaussian
elimination. See LPCSolve().
However the autocorrelation system of equations can be solved much more
efficiently since the autocorrelation coefficients in the matrix form of the
equations have a very simple and symmetric structure. This allows for a recursive solution procedure in which each
predictor coefficient may be derived in turn and used to calculate the next
coefficient. This is the dominant
method for solving the linear prediction equations, and is usually credited to
Levinson and Durbin. See LPCAutocorrelation().
Spectrum Modelling
The determination of the b
coefficients from some section of signal provides us with an all-pole filter
that characterises the source on the assumption that the input signal is white
(i.e. has a flat spectrum). Thus the
frequency response of the derived filter gives a smooth model of the signal
spectrum under the predictor assumptions.
See Example program 9.2.
Bibliography
T. Parsons, Voice and Speech Processing, McGraw-Hill 1987, Ch 6.
Markel & Grey, Linear Prediction of Speech, Springer-Verlag,
1976.
Algorithms
Algorithm 8.1 Linear
Prediction Solution - Direct Method
|
// lpcsolve.cpp - elementary solution of LPC equations // // C++ © 1996 Mark Huckvale University College London #include “tools.h” #include “ltisys.h” #include “lpcsolve.h” // smallest allowable value const double EPSILON=1.0E-10; // Solve set of simultaneous linear equations // by Gauss-Jordan elimination double MatrixSolve( Equation *mat, // matrix of equations: n rows x (n+1) cols int n // matrix size ) // returns determinant { double det=1.0; // determinant // Gauss-Jordan elimination for (int i=1;i<=n;i++) { // for each row // find pivot row from max column entry double max = 0; // maximum value in column int pos = 1; // position of pivot column for (int j=i;j<=n;j++) if (fabs(mat[j][i]) > max) { max = fabs(mat[j][i]); pos = j; } // check for column of zeros if (max < EPSILON) return(0.0); // transpose current row with pivot row // and normalise diagonal element to unity max = mat[pos][i]; for (int j=1;j<=n+1;j++) { double temp = mat[pos][j]; mat[pos][j] = mat[i][j]; mat[i][j] = temp/max; } // keep record of determinant if (i!=pos) det = det * -max; else det = det * max; // reduce matrix by dividing through by row for (int k=1;k<=n;k++) if (k!=i) { double val = mat[k][i]; for (int j=i;j<=n+1;j++) mat[k][j] = mat[k][j] - val * mat[i][j]; } } // return determinant return det; } |
|
// set up and solve LPC equations int LPCSolve( Waveform x, // windowed input signal int order, // predictor order required LTISystem& ltis // returned predictor coefficients ) // returns 0=OK, 1=zero power, 2=fail { // compute autocorrelations double *r = new double[order+1]; for (int i=0;i<=order;i++) { double sum = 0; for (int k=1;k<=x.count()-i;k++) sum += x[k] * x[k+i]; r[i] = sum; } // build set of linear equations Equation *mat = new Equation[order+1]; // builds NxN+1 matrix for (int i=1;i<=order;i++) for (int j=1;j<=order;j++) mat[i][j] = r[abs(i-j)]; for (int i=1;i<=order;i++) mat[i][order+1] = -r[i]; // free autocorrelation array delete [] r; // solve them if (MatrixSolve(mat,order)==0) { delete [] mat; return -1; // fail } // copy coefficients into LTI System ltis = LTISystem(0,order); ltis.a[0] = 1.0; for (int i=1;i<=order;i++) ltis.b[i] = mat[i][order+1]; // OK delete [] mat; return 0; } |
Algorithm 8.2 Linear
Prediction Solution - Autocorrelation Method
|
// lpcauto.cpp - compute linear predictor coefficients by autocorrelation // // C++ © 1996 Mark Huckvale University College London #include “tools.h” #include “ltisys.h” #include “lpcauto.h” // LPCAutocorrelation() Form autocorrelation vector and then // solve the normal equations using the // Levinson (Durbin) recursion // Translated from the routine LPCA written in FORTRAN // by T.Parsons “Voice and Speech Processing” McGraw-Hill 1987 |
|
int LPCAutocorrelation( Waveform x, // windowed input signal int order, // predictor order required LTISystem& ltis, // returned predictor coefficients double& pe // returned predictor error ) // returns 0=OK, 1=zero power, 2=fail { // compute autocorrelations double *r = new double[order+1]; // temporary array for (int i=0;i<=order;i++) { double sum = 0; for (int k=1;k<=x.count()-i;k++) sum += x[k] * x[k+i]; r[i] = sum; } // check power in signal if (r[0] == 0) { delete [] r; return 1; // no signal !! } // compute predictor coefficients double *pc = new double[order+1]; // temporary array pe = r[0]; // initialise error to total power pc[0] = 1.0; // first coefficient (b[0]) must = 1 // for each coefficient in turn for (int k=1;k<=order;k++) { // find next coeff from pc[] and r[] double sum = 0; for (int i=1;i<=k;i++) sum -= pc[k-i] * r[i]; pc[k] = sum/pe; // perform recursion on pc[] for (int i=1;i<=k/2;i++) { double pci = pc[i] + pc[k] * pc[k-i]; double pcki = pc[k-i] + pc[k] * pc[i]; pc[i] = pci; pc[k-i] = pcki; } // calculate residual error pe = pe * (1.0 - pc[k]*pc[k]); if (pe <= 0) { delete [] r; delete [] pc; return 2; // no power left in signal! } } // copy coefficients into LTI System ltis = LTISystem(0,order); ltis.a[0] = 1.0; for (int i=1;i<=order;i++) ltis.b[i] = pc[i]; delete [] r; delete [] pc; return 0; // return OK } |
Example
Programs
Example
8.1 Demonstration of Linear
Prediction
|
// lpcaut_t.cpp - test LPCAutocorrelation() #include "tools.h" #include "ltisys.h" #include "lpcauto.h" // constants const int WINDOWSIZE=32; const int NCOEFF=4; const double C1=0.16,C2=-0.12,C3=0.08,C4=-0.04; int main() { Waveform iwin(WINDOWSIZE,1); // make a test signal from recursive filter iwin[1] = 0.75; // put in pulse of power sqr(0.75) for (int i=2;i<=WINDOWSIZE;i++) iwin[i] = -C1 * iwin[i-1] - C2 * iwin[i-2] - C3 * iwin[i-3] - C4 * iwin[i-4]; // exploits bad index capability // do LPC analysis LTISystem osys(0,0); double pe; if (LPCAutocorrelation(iwin,NCOEFF,osys,pe)==0) { cout << "Predictor coefficients:\n"; for (int i=1;i<=NCOEFF;i++) cout << "Coeff " << i << " = " << osys.b[i] << "\n"; cout << "Residual error = " << pe << "\n"; } else cerr << "LPC analysis fails\n"; } |
Output from lpcaut_t.cpp:
|
Predictor coefficients: Coeff 1 = 0.16 Coeff 2 = -0.12 Coeff 3 = 0.08 Coeff 4 = -0.04 Residual error = 0.5625 |
Example 8.2 Linear Prediction Spectrum
|
// lspect_t.cpp - demonstrate LPC spectrum #include "tools.h" #include "quantise.h" #include "ltisys.h" #include "cfft.h" #include "window.h" #include "annot.h" #include "lpcauto.h" const char *FILENAME="/users/mark/trial"; const char *SPITEMNO="sp"; const char *ANITEMNO="an"; const char *ANLABEL="I"; // load waveform sample from test signal Waveform ReadSample() { // read in annotation AnnotationList anlist; if (anlist.load(FILENAME,ANITEMNO)!=0) { cerr << "Could not find annotations\n"; exit(0); } // find annotation Annotation an = anlist.find(ANLABEL); if (!an.name) { cerr << "Could not find annotation\n"; exit(0); } // load appropriate section Signal isig(1,1.0); isig.load(FILENAME,SPITEMNO,an.posn,an.size); // convert to waveform Waveform iwv = MakeCont(isig,0.001); return iwv; } int main() { // set up graphs Graph gr(3,1,"LPC Spectrum"); // load sample waveform Waveform iwv = ReadSample(); // window with Hamming window iwv = Hamming(iwv); // plot waveform iwv.plot(gr,1,"Speech Sample"); // perform FFT on windowed signal ComplexWaveform cwv = WaveformToComplexWaveform(iwv); Spectrum sp = ComplexFFT(cwv); // plot FFT spectrum (sp.half()).plotLogMag(gr,2,"DFT Spectrum"); |
|
// perform LPC Analysis int ncoeff = 2+(int)(iwv.rate()/1000); // rule of thumb LTISystem osys(0,0); double pe; if (LPCAutocorrelation(iwv,ncoeff,osys,pe)==0) { // calculate frequency response of filter Spectrum fresp(500,1000/iwv.rate()); for (int i=0;i<500;i++) fresp[i] = osys.response(i/1000.0); // plot frequency response fresp.plotLogMag(gr,3,"LPC Magnitude Response"); } gr.close(); } |
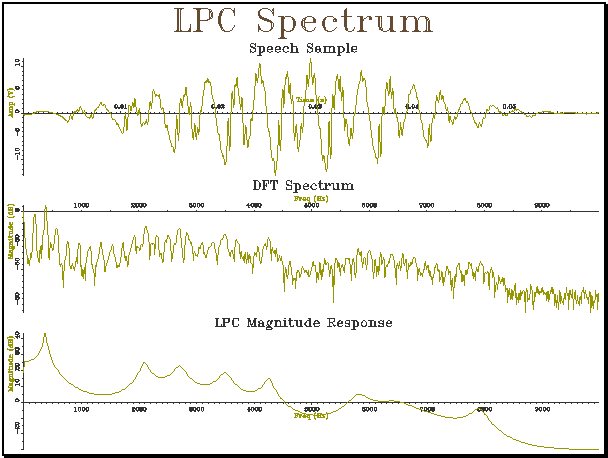
Exercise
8.1 Generate a whispered vowel by passing
noise through 3 resonators at say 500, 1500 and 2500Hz (with 100Hz bandwidths)
and then use LPC to estimate the frequencies of the resonators from the
signal. Display the signal, the FFT
spectrum and the LPC spectrum as in Example 8.2. How might you find the exact locations of the peaks in the LPC
spectrum?