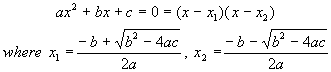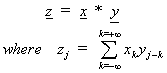UNIT
2:
MATHEMATICAL
ENVIRONMENT
2.1 Introduction
This
unit introduces some basic mathematical concepts and relates them to the C++
notation used in the course.
When
you have worked through this unit you should:
·
appreciate that a mathematical formalism can be
expressed in an algorithmic language like C++ as a procedure or function.
·
know how array indexing is formalised in the notes and
programs
·
know how complex numbers arise and how to perform
basic arithmetic on complex numbers
·
understand the special characteristics of the
multiplication of complex numbers when expressed in polar form
·
know how to represent polynomials as a coefficient
series and as a set of roots
2.2 Relating
algebra to algorithms
The mathematical notation used to describe signal
processing involves scalars, complex numbers and vectors; it exploits
operations of addition, subtraction, multiplication and division, as well as
exponents, logarithms, indexing and summation.
Each of these elements of mathematical notation have equivalents in the
C++ computer language implementation.
Consider the formal expression for the calculation of the
roots of a quadratic (the values of x where the equation is zero):
|
|
To map such mathematical notation onto a computer
program, we need to identify the inputs and constants, the outputs and
intermediary values, the operations and procedure of calculation. In this example the inputs are the constants
a b c, the output x1 x2, the operations + -
* / sqrt, and the procedure one of computing the expressions for the roots and
their assignment to the variables x1 and x2. With a procedural wrapper:
void findquadroot(double
a,double b,double c,double& x1,double& x2)
{
x1 = (-b + sqrt(b*b -
4*a*c))/(2*a);
x2 = (-b - sqrt(b*b -
4*a*c))/(2*a);
}
Where the notation double& indicates the values that are returned to the calling
program. Note that this version will
fail for quadratics where 4ac > b2.
To manipulate signals as entities, we need to represent
them as vectors, that is as an array
of simple scalar values. We also need
to be able to identify single elements (samples) of the vector by subscripting
or indexing. Although in conventional mathematical notation
we might write a vector symbol as x,
its expansion as (x1, x2, ... ,xN) and an
element of the vector as xk, in this course we choose:
vector: x[]
expansion: x[1], x[2], ..., x[N]
element: x[k]
This allows a straight-forward mapping to the C++
notation for arrays and array indexing.
Consider the conventional mathematical expression for
convolution. This takes two vectors,
and returns a third which is a kind of vector product:
|
|
In this course such a formula would be expressed in terms
of a procedure that takes signals x[] and y[] and calculates each output sample
z[j] using:
|
|
Here we not only simplify the notation but incorporate
standard assumptions such as that signals are indexed from time 1, and are zero
at earlier times.
This formulation leads to a natural C++ implementation:
void convolution(Waveform
x,Waveform y,Waveform& z){
{
for (int
j=1;j<=y.count();j++) {
z[j] = 0;
for (int
k=0;k<j;k++)
z[j] +=
x[k+1] * y[j-k]
}
}
The only difficult part with this translation is the
selection of the upper limit for k in the summation loop,
which should not be allowed to access samples before the start of the y[]
signal. We also assume that x[] is at
least as long as y[].
2.2 Complex
numbers
The fact that there are equations
such as
|
|
which are not satisfied by any real value for x, leads to
the introduction of complex numbers. A
complex number is an ordered pair of real numbers, usually written in the
convenient form x + iy, where x and y
are real numbers. Complex numbers are
subject to rules of arithmetic as defined below. We can of course refer to a complex number by a single
algebraical variable, say z:
|
|
The symbol i is
called the imaginary unit (in
engineering texts, it is sometimes referred to as j). The number x is called the real part of the complex number z
and y is called the imaginary part of z. Thus the solutions for
the equation x2 - 4x + 13 = 0, may be written:
|
|
Complex numbers can be represented as points on a plane
where the horizontal or x-axis is called the real axis, and the vertical or
y-axis is called the imaginary axis.
Complex numbers are then points in a cartesian co-ordinate system on
this plane, which is sometimes called the complex
plane.
Two complex numbers
|
|
are defined to be equal
if and only if their real parts are equal and their imaginary parts are equal,
that is
|
|
Relational expressions between complex numbers, such as z1
< z2, have no meaning, although the magnitudes of complex numbers
may be compared, see below.
Addition. The sum z1 + z2 is
defined as the complex number obtained by adding the real and imaginary parts
of z1 and z2, that is
|
|
This addition is like the addition of vectors on the
Cartesian plane.
Subtraction. The sum z1 - z2 is
just the inverse of addition, that is
|
|
Multiplication. The product z1z2 is
defined as the complex number
|
|
which is obtained by applying the normal rules of
arithmetic for real numbers, treating the symbol i as a number, and replacing i2
= ii by -1.
Division. This is defined as the inverse operation of multiplication;
that is the quotient z = z1/z2 is the complex number z =
x + iy which satisfies
|
|
For which a solution may be found by equating real and
imaginary parts, assuming that x2 and y2 are not both
zero:
|
|
Expressions. For any complex numbers z1, z2,
z3 we have:
z1 + z2
= z2 + z1 and z1z2 = z2z1 Commutative
laws
(z1 + z2)
+ z3 = z1 + (z2 + z3) and (z1z2)z3
= z1(z2z3) Associative laws
z1(z2
+ z3) = z1z2 + z1z3 Distributive
law
Conjugation. If z = x + iy is any complex number, then x - iy is called the conjugate
of z, and is denoted by z*. The product
of a complex number with its conjugate is a purely real number:
|
|
Any complex number of the form x + i0 is just the real number x.
Any complex number of the form 0 + iy
is called a pure imaginary number.
Polar form of complex
numbers. If we
introduce polar co-ordinates r, q in the
complex plane by setting x = r cos q, y = r
sin q, then
the complex number z = x + iy may be
written
|
|
This is known as the polar form of the complex number
z. The value r is called the absolute value or modulus of z, denoted by |z|.
Thus
|
|
The directed angle measured from the positive x axis to
the direction of the complex number from the origin of the complex plane is
called the argument of z, denoted by
arg z. Angles are always measured
counterclockwise and in radians. Note:
|
|
By application of standard addition theorems of
trigonometry we find the following relations for the polar form of the product
of two complex numbers
|
|
That is the magnitude of the product is the product of
the input magnitudes, and the argument of the product is the sum of the input
arguments. From these we can obtain the
important result for the polar form of the powers of a complex number
|
|
This reduces to the so-called De Moivre formula for unity magnitude z:
|
|
From this we can see that the sequence of powers of a
complex number of magnitude 1 are simply a sequence of counter-clockwise
rotations by q around
the origin on the complex plane.
Complex exponential. The exponential of a real number x, written
ex or exp x, has the series expansion:
|
|
The exponential function for complex z = x + iy is denoted by ez and
defined in terms of the real functions ex, cos y and sin y, as
follows:
|
|
From this we obtain the Euler formula for imaginary z:
|
|
This in turn leads to the following important identities:
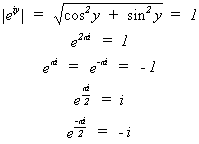
The complex numbers eiq, 0<q<2p lie on
the unit circle of the complex plane; and the values 1, i, -1, -i are the points
where the unit circle crosses the axes.
2.3 Polynomials
The Z-transform of a signal, which we will meet later, is
a way of expressing a time series of samples as a single mathematical object: a
polynomial in the variable z where
the coefficients of the polynomial are simply the sample values. Here we consider some basic operations on
polynomials.
In its simplest form a polynomial may be expressed
|
|
where the size of the polynomial n is called the order of
the polynomial, and the constants a0, a1, etc are called
the polynomial coefficients. Note that
this expression may also be written
|
|
Operations such as addition, subtraction, multiplication
and division may be performed on polynomials by elementary arithmetic and the
collection of terms of equivalent powers of x.
For multiplication, the product of a polynomial p of order m with a
polynomial q of order n is a polynomial of order m+n.
The division of a polynomial of order m by a polynomial of order n
(where n < m), leaves a polynomial or order m-n and a remainder of degree n-1.
Polynomials may be reduced into a product of factors; a polynomial p(x) of order n having n factors:
|
|
For many purposes it is more convenient to work with the
coefficients b than the polynomial
coefficients a. This is because it easy to see that the
values b are also the values of x for which the polynomial has the value
0. Thus the b coefficients are also called the roots of the polynomial p(x).
A polynomial of order n
must have n roots, but these may not
all be real. However if the
coefficients of p(x) are real, any complex valued roots must occur in complex
conjugate pairs. For polynomials of an
order > 4, there exists no formula which directly calculates the values of
the roots from the a coefficients,
and so iterative numerical methods need to be used.
Finally, there is a close relationship between the form
of polynomials and the form of power
series approximations to functions.
Here we just give some series expansions of some functions that may be
of use later in the course:
|
|
|
|
|
|
|
|
|
|
|
Exercise
2.1 Use the Complex class to implement a function that will solve arbitrary quadratic equations. In particular, write a program to accept the coefficients a, b and c, and which prints out the values of the two roots in complex notation. |