Construction of a Digital Resonator

1. z-plane description

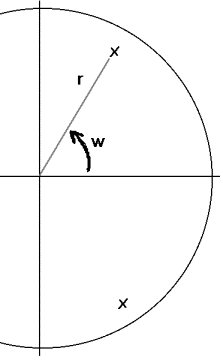
A digital resonator is a recursive (IIR) linear system having a complex conjugate pair of poles located inside the unit circle of the z-plane.

The angle of the poles in polar co-ordinates sets the resonant frequency of the resonator, while the distance of the poles are to the unit circle sets the bandwidth. The closer they are to the unit circle, the smaller the bandwidth.

We first seek an expression for the z-plane location of the poles, then expand the expression for the linear system to obtain the b[] coefficients.

2. Pole location

Angle to pole, w = 2pf where f is resonant frequency expressed as fraction of sampling rate.

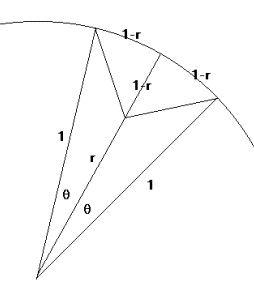
To find r from bandwidth, find the 3dB points on unit circle. These need to be Ö2 further away from the pole than the unit circle.

Therefore have triangles of sides (1-r), (1-r) and Ö2(1-r) between pole and 3dB points.

We can then see that:

sin(q) = 1 - r

and since q is small and equal to half the bandwidth:

r » 1 - b/2

where b is bandwidth expressed in radians.

3. Form difference equation

Poles are at r(cos(w)+isin(w)) and r(cos(w)-isin(w)).

So H(z) = 1/(1-r(cos(w)+isin(w))z^-1)(1-r(cos(w)-isin(w))z^-1)

Expanding:

H(z) = 1/(1 - 2rcos(w)z^-1 + r²z^-2)

Therefore coefficients are:

a₀ = 1

b₀ = 1

b₁ = -2rcos(w)

b₂ = r²

MAH

8Nov97