UNIT
3:
DIGITAL
WAVEFORMS
Summary
This unit is concerned with the representation and
measurement of signals as digital waveforms: specifically with sampling,
quantisation, the measurement of energy and the generation of sine and noise
signals.
When you have worked through this unit you should:
·
understand the concept of sampling
·
know the limits to the setting of sampling frequency
·
be able to state the sampling theorem
·
be able to explain how and why aliasing occurs
·
understand the concept of quantisation
·
be able to explain the origin of quantisation noise
·
understand how sinewaves and noise waveforms can be
generated by a program
·
have tried to create programs to build and replay
waveforms to specification
Concepts
Sampling is the
process whereby an analogue signal (continuous in time and continuous in value)
is converted to a series of impulses of a size equal to the amplitude of the
signal at regularly spaced instants of time.
Related ideas are the sample period
(T): the time between samples expressed in seconds, and sampling frequency (Fs=1/T):
the number of samples taken per second of signal, usually expressed in units of
samples per second or less accurately and more commonly in hertz (Hz).
Quantisation is the
process of converting the sampled analogue signal (discrete-time continuous
value) into impulses of discrete values of amplitude (analogous to the
conversion from 'floating-point' values to 'integer' values in a program). Related ideas are quantisation error: the error in amplitude estimate introduced by
quantisation, and quantisation noise:
the noise introduced into a quantised signal by the approximation of the
quantisation to the real analogue values.
The most common forms of quantisation are linear and produce a binary code conveniently described in terms of
numbers of bits. Each bit approximates
to 6dB of additional signal/noise improvement.
However, non-linear quantisation schemes are also used, primarily in
telecommunication systems to make the best use of available capacity. In a logarithmic quantisation scheme, the
amplitude levels are further apart at large amplitudes and closer at smaller
amplitudes, thereby giving a quantisation error which is proportional to the
size of the signal at that instant.
The sampling
theorem (of Nyquist and Shannon) states that a signal which has a highest
frequency component of f Hz must be sampled at a rate of at least 2f Hz if the
signal is to be faithfully reconstructed from the digital samples. The consequence of not following the
sampling theorem is aliasing, whereby
the spectral components above f Hz are 'mapped' down to the frequency region
0..f Hz by the sampling process thereby distorting the representation. To prevent aliasing a pre-sampling or anti-aliasing
filter is used to remove spectral components above half the sampling frequency;
this is usually implemented as a low-pass filter of high order, with a corner
frequency a little less than half the sampling frequency. A similar low-pass reconstruction filter is also used in digital-to-analogue
conversion, to rebuild the analogue waveform from the digital samples in the
frequency region 0..f Hz only.
To demonstrate formally that a sampled signal has many
possible aliases as continuous waveforms, consider the sampled sinusoid:
![]()
where W controls the frequency of the sinusoid (there
are 2p/W samples per period). Consider
the sequence y1[n] obtained by increasing W by 2p:
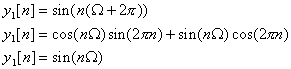
In other words, the same sequence as
x[n]. Similarly the sequence y2[n]
given by:
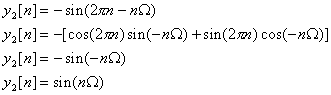
is also identical with x[n].
The
value W is just the angular change per sample, expressed in radians. To convert this to a basis in time, we set W = wT, where T is the sample interval, and w is the angular
frequency expressed in radians per second.
w is related to conventional frequency f (in hertz) by w = 2pf. When
f = Fs, then W = 2p. From
this we can see that the aliases of a sinusoid at a frequency f are just mFs+f and mFs–f, (m is some integer), since:
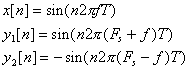
The total energy
in a digital waveform is simply the sum of the squared amplitude values, the average energy is the total energy
divided by the number of samples, and the r.m.s.
amplitude is the square root of the average energy. For a sine wave, the r.m.s. amplitude is
just the peak amplitude/Ö2.
Algorithms
Sinewaves
can be constructed from the sin() function provided in the ‘C’
language. Noise signals can be
generated through the use of the 'C' function random().
Algorithm 3.1 Sampling a sinusoid
|
// sampsine.cpp -- Sampling of Sinusoids // // SampleSine() retrieve samples from sine wave // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "sampsine.h" double SampleSine( double freq, // sine frequency (Hz) double amp, // sine peak amplitude double phase, // sine phase (degrees) double time // sample time = // sample # * sample period ) // returns sample value { // angular frequency (radians/sec) double rfreq = 2.0 * PI * freq; // phase in radians double rphase = 2.0 * PI * phase / 360.0; // sample sine function return amp * sin(rfreq * time - rphase); } |
Algorithm 3.2 Quantisation
|
// quantise.cpp -- Linear Quantisation (Real <-> Integer) // // QuantiseSample() linear quantisation // Quantise() linear quantisation of waveform // MakeCont() make quantised signal continuous // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "quantise.h" int QuantiseSample( double value, // input value double quanta // quantisation step ) // returns quantised sample { // truncate towards 0 return (int)(value/quanta); } Signal Quantise( const Waveform& iwv, // real-valued waveform double quanta // quantisation step ) // returns quantised signal { Signal owv(iwv.count(),iwv.rate()); for (int i=0;i<owv.count();i++) owv[i] = QuantiseSample(iwv[i+1],quanta); return owv; } Waveform MakeCont( const Signal& iwv, // quantised signal double quanta // quantisation step ) // returns real-valued signal { Waveform owv(iwv.count(),iwv.rate()); for (int i=1;i<=owv.count();i++) owv[i] = iwv[i-1] * quanta; return owv; } |
Algorithm 3.3 Sampling a noise signal
|
// noise.cpp -- generate noise samples // // SampleNoise() generate samples from white noise source // with a Gaussian (normal) amplitude distribution // // C++ (c) 1996 Mark Huckvale University College London #include <stdlib.h> #include <math.h> #include "noise.h" double SampleNoise( double amp // peak amplitude ) // returns noise sample { // get a random co-ordinate inside the unit circle double x,y,r; do { x = (random()%1000000)/500000.0 - 1.0; y = (random()%1000000)/500000.0 - 1.0; r = (x*x)+(y*y); } while ((r == 0) || (r >= 1.0)); // transform into a normal distribution // (Box-Muller transform) double rval = x * sqrt(-2.0*log(r)/r); // return scaled sample return amp * rval; } |
Bibliography
Rosen & Howell, Signals and
Systems for Speech and Hearing, Chapter 14.
Meade & Dillon, Signals and
Systems, Chapter 1.
Lynn & Fuerst, Introductory
Digital Signal Processing, Sections 1.1-1.4.
Orfanidis, Introduction to Signal Processing, 1.1-1.4.
Example Programs
Example 3.1 Demonstrate Sampling and Quantisation
|
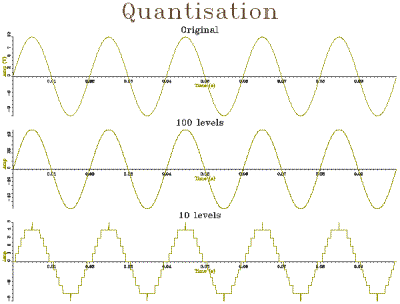
// sample_t.cpp -- demonstrate sampling and quantisation #include "tools.h" #include "quantise.h" #include "sampsine.h" const double SAMPRATE=10000.0; // sample/sec const int WAVESIZE=1000; // # samples const double SINEFREQ=50.0; // Hz const double SINEAMP=10.0; // volts const double SINEPHASE=0.0; // degrees int main() { // create a sine wave Waveform rwv(WAVESIZE,SAMPRATE); for (int i=1;i<=WAVESIZE;i++) rwv[i] = SampleSine(SINEFREQ,SINEAMP, SINEPHASE,i/SAMPRATE); // quantise Signal qwv1 = Quantise(rwv,0.2); // 100 levels Signal qwv2 = Quantise(rwv,2.0); // 10 levels // display Graph gr(3,1,"Quantisation"); rwv.plot(gr,1,"Original"); qwv1.plot(gr,2,"100 levels"); qwv2.plot(gr,3,"10 levels"); gr.close(); } |
Example 3.2 Demonstrate noise signal generation and replay
|
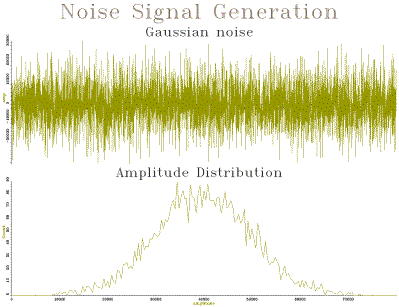
// noise_t -- generate and replay noise signal #include <iostream.h> #include "tools.h" #include "quantise.h" #include "noise.h" const double SAMPRATE=10000.0; // samples/sec const double QUANTA=0.001; // 1mV/level const int WAVESIZE=5000; // 0.5 seconds const double WAVEAMP=10.0; // +/- 10V int main() { int i,idx; // create empty waveform Signal nwv(WAVESIZE,SAMPRATE); // store noise samples for (i=0;i<WAVESIZE;i++) nwv[i] = QuantiseSample(SampleNoise(WAVEAMP),QUANTA); // plot waveform Graph gr(2,1,"Noise Signal Generation"); nwv.plot(gr,1,"Gaussian noise"); // calculate and plot amplitude histogram WaveDouble hist(201,0.0025); for (i=0;i<WAVESIZE;i++) { // map -40000..40000 to 0..200 idx = (nwv[i]+40000)/400; // keep count hist[idx] = hist[idx] + 1.0; } hist.plot(gr,2,"Amplitude Distribution","Amplitude","Count"); gr.close(); } |
Exercises
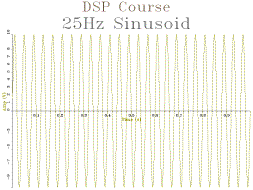
3.1 Use example program 3.1 to construct a program to display 1s of a sinewave signal of 25Hz sampled at 1,000 samples per second.
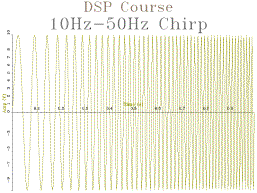
3.2 Adapt your program from exercise 3.1 to display a sine signal that increases linearly in frequency from 10Hz to 50Hz over an interval of 1 second.
3.3 Adapt your program from exercise 3.1 to construct and display 1s of a 10Hz square wave made up from the sum of 16 odd harmonics. The relative amplitude of the nth harmonic is given by 1/n, i.e. H1 + 0.33H3 + 0.2H5 + …, or
![]()