SFS/ESystem
Signals & Systems Tutorial

by Mark Huckvale

_Program:	_{Vs 1.1}
_Tutorial:	_{Vs 1.1}

Contents:
¤Basics
¤Spectrum
¤Systems
¤Vowels
¤Digital Systems
¤Learn More
¤Feedback
¤Copyright

Internet links:
¤ESystem Home
¤SFS Home
¤Speech &
Hearing Home
¤UCL Phonetics
and Linguistics

ESystem is a learning environment for the theory of signals and systems. With ESystem you can study how signals can be characterised and measured; study how systems can be described; and study what systems do to signals that pass through them. ESystem is a kind of workbench which allows you to select from a range of input signals and pass them through a range of systems so that you can see the effects of each system on their waveform, their spectrum, and their sound.

This tutorial uses the ESystem program to help you learn about signals and systems theory. Look at the Learn More section for recommendations of text books and other related learning materials.

To get the most from the tutorial arrange the windows on the desktop so that you can see the ESystem program window and this tutorial at the same time.

1. Basic Operation

Creating and playing a sound
In this example you will create a "buzz" sound and replay it.
- Choose menu option Input/Pulse Train.
- In the frequency box enter the value 100, and click OK.
- Click the mouse on the graph labelled "Input Signal".
You should hear a low-pitched buzz sound replayed. Adjust the volume control on your computer and/or the speaker so that this is at a comfortable level. The computer volume control can sometimes be found by clicking on the loudspeaker icon in the system tray at the bottom right of the screen. The Input Signal graph plots the amplitude of the signal as a function of time. You should see that it is made up from a series of short spikes or "pulses". This graph is also called a waveform. It shows the change in size of the electrical signal sent to the loudspeaker, the movement of the speaker cone, and the change in air pressure caused by movement of the speaker cone. This change in air pressure propagates through the air to your ears, your eardrums move in and out following the change in pressure, and you get to hear the sound.

Test your understanding

What is meant by a "waveform"? A waveform is a graph of how the amplitude of a signal changes with time.

Configuring a system to change the loudness of the sound

In this example you will set up an amplifier to change the overall amplitude of the signal you've just created.

Choose menu option System/Amplifier
In the Gain box enter the value 6, and click OK.
Study the difference between the Input Signal graph and the Output Signal graph
Replay the Input Signal and then the Output Signal by clicking first on the Input Signal graph, then on the Output Signal graph.

An amplifier with a gain of 6dB increases the amplitude of signals passed through it by a factor of 2. If you look at the bottom right of the ESystem screen, you will see a display of the input and output peak amplitudes which confirms that the amplifier has doubled the size of the input. You should also hear that the output signal is louder than the input signal. The amplifier has increased the size of the signal sent to the loudspeaker, and hence increased the size of the air pressure variations picked up by your ears.

Test your understanding
How would the sound change if instead of doubling the size of the signal, the amplifier halved the size of the signal?	The signal would sound quieter after it had passed through the system.

Changing the pitch of the sound

In this example you will change the perceived pitch of the buzz sound by changing its repetition frequency.

Choose menu option Input/Pulse Train.
In the frequency box enter the value 200, and click OK.
Replay the Input Signal by clicking the mouse on the graph labelled "Input Signal".

The number you put in the frequency box sets the repetition frequency of the sound (this is also known as the sound's fundamental frequency). In the first example, we set the repetition frequency of the pulse train to 100Hz, that is 100 pulses per second. This gave a relatively low-pitched sound. Here we doubled the repetition frequency to 200Hz, so now there are twice as many pulses being generated per second. You should see that the pulses are now closer together in time than before. Adjust the repetition frequency to 400Hz and then to 800Hz to see how the waveform and the sound changes. The steps 100, 200, 400 and 800 are called one octave changes in pitch. A pitch interval of an octave corresponds to a change by a factor of two in repetition frequency.

Test your understanding
How is the loudness and pitch of a sound related to its waveform?	Loudness is related to the size of the signal (its amplitude) while pitch is related to how many times the signal repeats per second (its repetition frequency).

Changing the timbre of the sound

In this example you will put the input signal through a system that changes the quality or timbre of the sound as it passes through.

Choose menu option Input/Pulse Train.
In the frequency box enter the value 100, and click OK.
Choose menu option System/Resonator.
In the Resonator System box, enter a Resonant Frequency of 1000Hz and a Resonant Bandwidth of 100Hz, and click OK.
Replay the Input Signal and the Output Signal and note the change in timbre.

Unlike the amplifier, the resonator system changes the shape of the input signal as it passes through. You will see that the output signal is no longer a series of short pulses. In fact each pulse seems to have been converted into a short vibrating sound. We hear this change in waveform shape as a change in timbre. Since the repetition rate of the sound has not been changed by the system, the pitch of the sound has not been changed.

Test your understanding
Can sounds change in timbre (quality) without also changing in loudness or pitch?	Yes. Two musical instruments can make the same note at the same loudness while still being recognisably different in quality. A trumpet and a clarinet for example.

2. The Spectrum

Sinewaves

In this example we will study how the spectrum graph shows us the properties of sinewaves.

Choose menu option Input/Sinewave.
In the frequency box enter the value 100, and click OK.
Choose menu option System/Amplifier
In the Gain box enter the value 0dB and click OK.
Click the mouse on the graph labelled "Input Signal".
Study the Input Signal graph and the Input Spectrum graph.

A 100Hz sinewave sounds like a low-pitched tone. You should be able to see the individual cycles of the sinewave on the input signal graph. It has a very smooth shape that goes positive and negative in equal amounts each cycle. At 100Hz each cycle lasts 10ms (=1/100s). Looking at the Input Spectrum display, you should see that this is showing low amplitude at all frequencies except 100Hz. The spectrum display is an analysis of a signal in terms of the amplitude of the sinewaves present in the signal. In this case the signal comprises exactly one sinewave of 100Hz. So the spectrum display shows that of all frequencies (i.e. sinewaves of different frequency) that could be present, only a sinewave at 100Hz is present in this signal.

Test your understanding
What three numbers are needed to define the waveform of a sinewave for all time?	Its amplitude: how big it is. Its frequency (or period): how many times it repeats per second (or how long one cycle lasts). Its phase: a record of where it has got to in its cycle at some known time.

Sinewaves of different frequency and amplitude

In this example we will see how the spectrum changes for sinewaves of different frequency and amplitude.

Choose menu option Input/Sinewave.
In the frequency box enter the value 1000, and click OK.
Choose menu option System/Amplifier
In the Gain box enter the value 6dB and click OK.
Listen to the Input Signal.
Study the Input Signal graph and the Input Spectrum graph.
Listen to the Output Signal.
Study the Output Signal graph and the Output Spectrum graph.

A 1000Hz sinewave sounds like a high-pitched tone. Because the repetition frequency is so high, it is difficult to see the individual sinewave cycles on the signal graphs. However the sinewave shape is much as before, just that there are 10 times as many of them per second. Since the input signal comprises exactly one sinewave at 1000Hz you should not be surprised that the Input Spectrum shows low amplitude for all frequencies except for the frequency of 1000Hz. We have put the input sinewave through an amplifier of gain 6dB which corresponds to a doubling in amplitude. You should see that the output waveform is about twice as large as the input waveform. The effect on the output spectrum is harder to see because the spectrum graphs use a logarithmic amplitude scale called decibels. However if you look closely you should see that the spectrum amplitude at 1000Hz has increased by 6dB from the input spectrum to the output spectrum. In summary then, the spectrum shows us what are the amplitude and the frequencies of the constituent sinewaves that make up a signal. The frequency of the component sinewaves is plotted horizontally across the screen, while the amplitude of the component sinewaves is shown vertically.

Test your understanding
How would the spectrum change if the signal comprised a mixture of two sinewave signals: one of 1000Hz and one of 2000Hz?	The spectrum would show two separate components: one at 1000Hz and one at 2000Hz. The spectrum analyses a signal into its constituent sinewave components.

Spectrum of a pulse train
In this example we will look at the spectrum of a pulse train signal.
- Choose menu option Input/Pulse Train.
- In the frequency box enter the value 400, and click OK.
- Listen to the Input Signal.
- Study the Input Signal graph and the Input Spectrum graph.
A pulse train with a fundamental frequency of 400Hz has 400 pulses per second, or one pulse every 2.5ms. You should be able to see this on the Input Signal graph. When we look at the Input Spectrum graph, we see that such a signal is actually made up from a number of sinewave components. You should be able to see that a pulse train at 400Hz has equal amounts of sinewaves at 400, 800, 1200, and all subsequent multiples of 400Hz. In other words, the waveform we see as a train of pulses can be equally constructed by adding together sinewaves at frequencies of 400Hz and multiples thereof. The sinewave components of a periodic sound like the pulse train are called harmonics. The sinewave component at 400Hz is the first harmonic of the pulse train; the sinewave component at 800Hz is the second harmonic of the pulse train; and so on. Since all harmonics occur at frequencies which are whole number multiples of the repetition frequency, the repetition frequency is also known as the fundamental frequency of the periodic signal.

Test your understanding

If we changed the fundamental frequency of the pulse train to 250Hz, what would be the frequency of the fourth harmonic? 1000Hz.
Relation between repetition period and harmonic spacing
In this example we will look at how the spectrum of a pulse train signal changes as its repetition frequency changes.
- Choose menu option Input/Pulse Train.
- In the frequency box enter the value 200, and click OK.
- Listen to the Input Signal.
- Study the Input Signal graph and the Input Spectrum graph.
- Choose menu option Input/Pulse Train.
- In the frequency box enter the value 800, and click OK.
- Listen to the Input Signal.
- Study the Input Signal graph and the Input Spectrum graph.
If we change the repetition frequency of the pulse train we change the size of the interval between one pulse and the next in the Input Signal graph. At 200Hz, the pulses are 5ms (1/200s) apart. At 800Hz, the pulses are 1.25ms (1/800s) apart. The duration of one cycle of a periodic signal is called its period. When the repetition frequency goes up, the repetition period goes down; indeed period = 1/frequency. Looking at the Input Spectrum graph however, we note that the frequency of the first harmonic is just the same as the repetition frequency. Furthermore the spacing between the harmonics is also the same as the repetition frequency. So when the repetition frequency increases, the harmonic spacing in the spectrum also increases. Taking these two observations together we see that as the repetition period decreases, the spacing between the harmonics increases.

Test your understanding

What would be the spacing between the harmonics of a pulse train consisting of pulses 20ms apart? 50Hz. 20ms = 0.02s = 1/50s.

Waveform and spectrum of another periodic sound

In this example we will look at the spectrum of a sawtooth waveform.

Choose menu option Input/Pulse Train.
In the frequency box enter the value 200, and click OK.
Listen to the Input Signal.
Study the Input Signal graph and the Input Spectrum graph.
Choose menu option Input/Sawtooth.
In the frequency box enter the value 200, and click OK.
Listen to the Input Signal.
Study the Input Signal graph and the Input Spectrum graph.

A sawtooth waveform is a periodic signal that looks like a sequence of right-angled triangles. This waveform also sounds like a buzz, but is less harsh than the pulse train. Looking at the Input Spectrum graph, you can see that both periodic sounds are made up from a small number of harmonics, here at multiples of 200Hz, the repetition frequency. In contrast to the spectrum of a pulse train at 200Hz, you should be able to see that the harmonics of a sawtooth are not all of equal amplitude; indeed the lower frequency harmonics have a greater amplitude than the higher frequency harmonics. It is this reduction in the amplitude of the high frequency components that makes a sawtooth signal sound less harsh than a pulse train signal. The utility of the spectrum graph is that it shows the characteristics of the signal that have consequences for our perception of the timbre of the sound.

Test your understanding
Two periodic signals have the same pitch but different timbres. What similarities and differences would we see between the two spectra of these signals?	The spectra would show components at the same harmonic frequencies but the components would have different amplitudes.

Waveform and spectrum of a single pulse

In this example we will look at the spectrum of a single pulse.

Choose menu option Input/Pulse Train.
In the frequency box enter the value 100, and click OK.
Study the Input Spectrum graph.
Repeat the above for frequencies of 50, 20 and 10Hz.
Choose menu option Input/Pulse.
Study the Input Spectrum graph.

A pulse train at 100Hz has harmonics which are spaced 100Hz apart. A pulse train at 50Hz has harmonics which are spaced 50Hz apart. A pulse train at 20Hz or 10Hz has harmonics which are spaced 20Hz and 10Hz respectively. You can see that as the period between one pulse and the next increases, the spacing between the harmonics decreases. A pulse train of 1Hz (not available in ESystem) would have harmonics spaced 1Hz apart. A single pulse, then, is just one part of a pulse train with a very long period - or in other words with a very low repetition frequency. A single pulse might be considered to have an infinite period and a repetition frequency of zero. Since the harmonic spacing is numerically the same as the repetition frequency, we should not be surprised to see the harmonics packed together into a single mass such that sinewave components occur at every frequency. This is what we see in the Input Spectrum graph of a single pulse. The spectrum of a single pulse is a horizontal line showing constant amplitude at all frequencies. i.e. a pulse has sinewave components at every frequency.

Test your understanding
A pulse is just one example of a signal that does not repeat. What spectrum characteristic is common to all signals that do not repeat?	Any non-periodic signal must have a continuous spectrum, that is, it would have some amplitude at all frequencies. This contrasts with periodic signals that only have amplitude at the harmonic frequencies.

Waveform and spectrum of a white noise

In this example we will look at the spectrum of white noise.

Choose menu option Input/White Noise
Listen to the Input Signal.
Study the Input Signal and Input Spectrum graphs.

White noise is a randomly changing signal that has approximately the same amount of energy at every frequency. Looking at the Input Signal graph, you should see that there is no repetitive structure visible. Indeed the change in amplitude of the signal from moment to moment is unpredictable and chaotic. White noise sounds like a rushing or hissing sound without any clear pitch. Looking at the spectrum of white noise you should be able to see that every sinewave component has approximately the same amplitude; and that components occur at every frequency. In some ways, the spectrum looks similar to the spectrum of a pulse: every frequency is represented in equal amounts. The spectrum as we have plotted it however, does hide the fact that the sinewave components in a pulse are all synchronised in phase, while the sinewave components in white noise have random and randomly changing phases.

Test your understanding
Why do you think that white noise is called "white"?	In an analogy to white light, which contains approximately equal amounts of every colour. White noise contains approximately equal amounts of every frequency.

3. Systems

Amplification and Attenuation

In this example we will use the amplifier system to increase and decrease the amplitude of a signal.

Choose menu option Input/White Noise.
Choose menu option System/Amplifier.
In the Gain box, enter 20dB.
Listen to the Input Signal and the Output signal.
Study the Input Signal and Output Signal graphs.
Choose menu option System/Amplifier.
In the Gain box, enter -20dB.
Listen to the Input Signal and the Output signal.
Study the Input Signal and Output Signal graphs.

The amplifier system changes the amplitude of a signal without changing its shape. A gain of 20dB is equivalent to an amplification of 10 times. You should see that the size of the Output Signal is ten times bigger than the size of the Input Signal. To convert linear amplification factors to decibels, use the formula: gain (dB) = 20 * log₁₀( factor). Thus a factor of 10 gives 20 * log₁₀(10) = 20 * 1 = 20dB.

A negative gain is equivalent to attenuation - a reduction in the amplitude of the signal as it passes through the system. A gain of −20dB means a reduction of 10 times. You should see that the Output Signal is ten times smaller than the input signal. The factor in this case, then, is x0.1. Gain (dB) = 20 * log₁₀(0.1) = 20 * −1 = −20dB.

Test your understanding
How would a signal change if it were passed first through one amplifier with a gain of 20dB and then through a second amplifier with a gain of −20dB?	The overall gain is 20dB + −20dB = 0dB. Thus the output signal would be the same size as the input signal.

Frequency Response

In this example we will look at the meaning of the Frequency Response graph.

Choose menu option Input/Pulse Train.
In the frequency box, enter 800Hz.
Choose menu option System/Low-Pass Filter.
In the frequency box, enter 2000Hz
Listen to the Input Signal and the Output signal.
Study the Input Spectrum, Frequency Response and Output Spectrum graphs.

The input signal has a repetition frequency of 800Hz and hence has harmonics at 800, 1600, 2400, and so on. In this example we have chosen to pass the signal through a system called a Low-Pass Filter. This system, as its name suggests, passes through unchanged sinewave components that are at a frequency lower than a given cut-off frequency, while reducing in amplitude sinewave components that are at a frequency higher than its cut-off frequency. We chose a cut-off frequency of 2000Hz in this example, so you should confirm that the harmonics at 800 and 1600Hz have indeed passed through the filter unchanged in amplitude. On the other hand, you should see that the third harmonic at 2400Hz has been attenuated by about 30dB, while higher harmonics at 3200Hz and above have been attenuated so much they do not even appear on the graph. The degree of attenuation of the filter as a function of frequency is plotted on the middle graph at the right, the Frequency Response graph. This graph shows how much the system amplifies or attenuates the sinewave components in an input signal. This graph characterises the system independently of any input signal. It tells us what the system does to sinewaves according to their frequency. Since all signals can be thought of as comprising a number of sinewaves, we can always predict what the consequences are for a signal passing through a system given the frequency response of the system. In linear units, we can calculate the output spectrum by multiplying the input spectrum by the frequency response. In decibel units this multiplication turns into addition. So you should be able to see that the output spectrum is nothing more than the sum of the input spectrum and the frequency response graph.

Test your understanding
Describe in words what is meant by the response of a system and what is shown by a frequency response graph.	The response of a system to an input signal is the ratio of the amplitude of the output signal to the amplitude of the input signal. The frequency response of a system describes how the value of the response of the system to sinewave signals varies as a function of their frequency.

Impulse Response

In this example we will look at the meaning of the Impulse Response graph.

Choose menu option View/Impulse Response.
Choose menu option Input/Pulse.
Choose menu option System/Resonator.
In the Resonator System box, enter a Resonant Frequency of 1000Hz and a Resonant Bandwidth of 100Hz, and click OK.
Listen to the Input Signal and the Output signal.
Study the Input Signal, Impulse Response and Output Signal graphs.

A simple resonator is a system that has a single preferred frequency of vibration. A pendulum or a mass hanging on a spring are examples of simple resonators. The resonator we have used here has a resonant frequency of 1000Hz. This means that of all possible frequencies of vibration, it most likes to vibrate at 1000Hz. You can confirm this by looking at the frequency response graph. This graph shows a single peak at 1000Hz. The interpretation of this is that we will get the biggest output from this system only if we put in a sinewave at 1000Hz - when the input frequency matches the resonant frequency. The Impulse Response graph shows this same fact in a different way. The impulse response graph shows what output waveform results if a pulse is input to the system. Putting a pulse in is exactly what we are doing in this example. You should see that the impulse response of a resonator is a "damped" sinewave at the resonant frequency. The impulse response graph of our resonator is a sinewave at 1000Hz which slowly decays in amplitude. The second parameter of a resonator is the bandwidth. This parameter sets the width of the peak on the frequency response graph. Here we set the peak width to be 100Hz at 3dB down from the peak. A wide bandwidth means the system responds well to a wide range of frequencies, while a narrow bandwidth means the system only responds well to a narrow range of frequencies. A wide bandwidth also corresponds to an impulse response that decays rapidly, while a narrow bandwidth corresponds to an impulse response that takes longer to die away. Try this out by setting the bandwidth of the resonator first to 300Hz (wide) and then 30Hz (narrow) to see the effect on the resonator frequency response and impulse response. In summary then, the impulse response is an alternative to the frequency response for characterising a system. While the frequency response tells us how the system process sinewaves of different frequencies; the impulse response tells us how the system responds to a single input pulse. In the frequency domain, we say that the output spectrum is formed by the product of the input spectrum and the frequency response. In the time domain we say that the output waveform is produced by the convolution of the input waveform with the impulse response. (We look at convolution in more detail in section 5).

Test your understanding
For a unit-sized input pulse going into a system, the output signal is numerically the same as the impulse response. What similar fact can you say about the output spectrum graph?	For a unit-sized input pulse going into a system, the output spectrum is numerically the same as the frequency response. This gives us one way of determining the frequency response of a system.

Response of Resonator to Sinewaves
In this example we will look more closely at how a simple resonator changes input sinewaves according to their frequency.
- Choose menu option System/Resonator.
- In the Resonator System box, enter a Resonant Frequency of 500Hz and a Resonant Bandwidth of 100Hz, and click OK.
- Choose menu option Input/Sinewave
- In the frequency box, enter 200Hz.
- Listen to the Input Signal and the Output signal.
- Study the change in the amplitude of the sinewave caused by the resonator.
- Repeat for frequencies of 400Hz, 600Hz and 800Hz.
You should first confirm that in all cases the output spectrum shows components at the same frequency as the input spectrum. Linear systems (the kind used by ESystem) cannot change the frequency of components, nor introduce new components. At 200Hz the gain of the resonator is only a little greater than 0dB. The output sinewave is very similar in amplitude to the input. At 400Hz the gain of the resonator is about 10dB, and the output amplitude is about 3 times bigger than the input. At 600Hz the gain of the resonator is about 6dB. At 800 Hz the gain of the resonator is about -5dB and the output amplitude is smaller than the input amplitude. A physical analogy might help explain what is going on here. Imagine you are shaking a pendulum at different frequencies. If you shake it very slowly (at a frequency well below its resonant frequency) then the output amplitude of the swings is much the same as the input amplitude. This corresponds to the first frequency we tried. As the frequency we shake the pendulum gets closer to its resonant frequency the larger the output amplitude. This corresponds to the second and third cases. However if we try and shake the pendulum at too high a frequency it fails to vibrate much at all, and the output amplitude is smaller than the input amplitude. This corresponds to the last case we tried. Try out other frequencies of your own. One final observation: look at the phase of the output waveform at time zero. When the input sinewave is at a frequency below the resonant frequency, the phase of the output roughly matches the input phase. However, at frequencies above the resonant frequency, the output phase is almost opposite to the input phase. This reminds us that systems can not only change the amplitude of sinewaves that pass through them, but can also change their phase.

Test your understanding

At what input frequency would we get the largest output amplitude? At 500Hz, which is the most preferred frequency of vibration of the resonator.

Response of Resonator to a Pulse Train

In this example we will look at how a simple resonator changes a pulse train in both time and frequency graphs.

Choose menu option System/Resonator.
In the Resonator System box, enter a Resonant Frequency of 500Hz and a Resonant Bandwidth of 100Hz, and click OK.
Choose menu option Input/Pulse Train
In the frequency box, enter 200Hz.
Listen to the Input Signal and the Output signal.
Study how the output signal is related to the input signal and impulse response graphs.
Study how the output spectrum is related to the input spectrum and frequency response graphs.

The impulse response of a simple resonator is a damped sinewave - here we see that it decays pretty rapidly and has almost disappeared after 10ms. The input signal is a sequence of pulses, one per 5ms. Each pulse triggers an impulse response of course. What we see in the output then is just a superposition of impulse responses, each response triggered by each input pulse. If you look closely you should see a repeating pattern in the output signal corresponding (approximately) to the first 5ms of the impulse response. Of course in reality the impulse responses overlap - as the resonator is still vibrating from one pulse by the time the next pulse comes in. The output spectrum shows that the original harmonics of the pulse train have been modified in amplitude as they passed through the resonator. In fact the first four harmonics are at just the same frequencies as we explored in the last example! We see that the first harmonic (200Hz) has barely changed in amplitude, while the second harmonic has changed by 10dB, the third by 6dB and the fourth by −5dB. These are the same values as we found for the independent sinewaves in the last example. This result confirms that the frequency response graph shows how a system modifies the size of sinewaves passing through it regardless of whether the sinewaves are passed independently or as part of a complex sound. This important result means that we can calculate the frequency response of a system by finding out how it responds to individual sinewaves of different frequency, but then we can apply the frequency response to complex signals.

Test your understanding
When you push a child on a swing a good strategy is to always push at the same point on each swing cycle, even if you don't push every cycle. How could you use Esystem to demonstrate that this strategy gives you the largest output amplitude?	Build a resonator at say 500Hz resonant frequency with a narrow bandwidth of say 25Hz. Look at the output amplitude for an input pulse train at 100Hz (one push per 5 swing cycles), 250Hz (1 push per 2 swing cycles), and 500Hz (one push per cycle). Compare with the output amplitude at 200Hz (one push per 2.5 cycles).

Response of a simple resonator to white noise
In this example we will look at the effect of a simple resonator on white noise.
- Choose menu option System/Resonator
- In the Resonator System box, enter a Resonant Frequency of 500Hz and a Resonant Bandwidth of 50Hz, and click OK.
- Choose menu option Input/White Noise.
- Listen to the Input Signal and the Output Signal.
- Study the how the output spectrum is related to the input spectrum and the frequency response graphs.
White noise is an aperiodic signal which has approximately the same amplitude at every sinewave frequency. When this signal is passed through the resonator, those sinewave components that are close to the resonant frequency are increased in amplitude, while those sinewave components far above the resonant frequency are reduced in amplitude. Because the output signal has a concentration of energy at 500Hz it gives a sensation of pitch similar to that of the pitch of a sinewave at 500Hz. Listen to the pitch of the filtered noise and then to a sinewave at 500Hz to confirm this. Move the resonator to 1000Hz and confirm that the filtered noise rises in pitch by one octave.

Test your understanding

Name a musical instrument that uses filtered noise to generate notes of different pitch. A flute, a recorder, or an organ are good examples.

Introduction to a band-pass filtering

In this example we will introduce the concept of a bandpass filter.

Choose menu option Input/Pulse Train
Set the frequency to 800Hz.
Listen to the input signal.
Choose menu option System/Low-Pass filter
Set the cut-off frequency to 2800Hz
Listen to the output signal.
Study which harmonics are changed in amplitude by the filter.
Choose menu option System/High-Pass filter
Set the cut-off frequency to 2000Hz
Listen to the output signal.
Study which harmonics are changed in amplitude by the filter.
Choose menu option System/Band-Pass filter
Set the low cut-off frequency to 2000Hz
Set the high cut-off frequency to 2800Hz
Listen to the output signal.
Study which harmonics are changed in amplitude by the filter.

An 800Hz fundamental frequency pulse train has harmonics at 800, 1600, 2400, 3200Hz and so on. It sounds like a harsh high-pitched buzz. When low-pass filtered at 2800Hz, only the lowest three harmonics are left with any significant amplitude. The sound loses its harshness after filtering. A high-pass filter is the reverse of a low-pass filter: it lets through unchanged frequency components above some cut-off frequency, while attenuating frequency components lower than the cut-off. A high-pass filter at 2000Hz removes the first harmonic and significantly weakens the second harmonic of our pulse train. The sound seems "thinner" and lacking in bass as a result. A band-pass filter is a kind of combination of a low-pass filter and a high-pass filter: it lets through unchanged only those components between two cut-off frequencies. In this case the bandpass filter is roughly a combination of the low-pass and high-pass filters we used before. The result of bandpass filtering between 2000 and 2800 is to leave a signal comprising almost only the third harmonic of our pulse train at 2400Hz. This signal sounds like a pure tone at 2400Hz just as we might expect.

Test your understanding
Explain the output signal you get if you pass a 200Hz sawtooth through a band-pass filter between 900 and 1300Hz.	The output signal is a combination of mainly the 5th and 6th harmonics. These two sinusoids are close in frequency and so "beat" together at their difference frequency of 200Hz. This explains the periodic pulsing in amplitude in the output signal.

Use of band-pass filter for signal analysis

In this example we will look at how a bandpass filter can be used to analyse the frequency content of a signal.

Choose menu option Input/Sawtooth
Set the frequency to 1500Hz.
Listen to the input signal.
Choose menu option System/Band-Pass filter
Set the low cut-off frequency to 250Hz
Set the high cut-off frequency to 750Hz
Record the size of the output signal ("Output Peak" in status bar).
Move the bandpass filter up by 250Hz (i.e. to 500-1000Hz).
Record the size of the output signal.
Repeat for frequencies 750-1250, 1000-1500, 1250-1750, 1500-2000, and so on, recording the output amplitude each time.
Plot a graph of the output amplitude against the center frequency of the band-pass filter. This is the kind of data you should plot:

Centre Freq Output Amp

500 1166

750 1294

1000 ...

... ...

The band-pass filter we have chosen is just 500Hz wide, while the spacing between the harmonics of the sawtooth is 1500Hz. When there is no overlap between the filter and any input harmonic, the output amplitude is very small. But when there is some overlap, there is significantly greater amplitude. The graph you plot should show the largest amplitude when the bandpass filter is centered over a harmonic. The graph you've plotted in fact is a graph of the amplitude of the input signal in a number of frequency regions - it bears a great deal of similarity to a spectrum! ESystem uses the same basic principle to draw the input and output spectrum graphs, although it uses a greater number of narrower filters than this example. In summary, band-pass filters can be used to analyse the frequency composition of a signal - we just plot the output amplitude of the filter as a function of its centre frequency over a number of frequency regions.

Test your understanding
True or False: our hearing uses band-pass filters to analyse the frequency content of sounds?	True. The cochlea contains a set of mechanical band-pass filters which allows nerve firing to be related to the amplitude of the signal in different frequency regions.

Simulation of a telephone channel

In this example we will band-pass filter a speech signal to simulate the kind of filtering performed by the telephone network.

Choose menu option Input/From File
Choose the input file "six.wav" (supplied with ESystem)
Listen to the input signal.
Choose menu option System/Band-Pass filter
Set the low cut-off frequency to 350Hz
Set the high cut-off frequency to 3500Hz
Listen to the output signal.

The band-pass filter removes both the very lowest frequencies and the very highest frequencies from the speech signal. The filtered signal has the characteristic quality of telephone speech - it is lacking in both bass and treble components. By reducing the bandwidth of the signal in this way, telephone companies are able to squeeze more conversations along each set of wires, making each conversation cost less to communicate.

Test your understanding
Why don't telephone companies choose an even narrower bandwidth to get even more conversations down one wire?	Further reductions in bandwidth start to significantly impact the intelligibility of the speech.

4. Generating Vowel-like sounds

Making a simple vowel
In this example we will generate a sound that is like the vowel in "word".
- Choose menu option Input/Pulse Train.
- Set the fundamental frequency to 100Hz.
- Choose menu option System/Vowel.
- Set the "formant" frequencies to 500, 1500 and 2500Hz.
- Listen to the input signal and the output signal.
- Study the frequency response graph.
In this example build a vowel-like sound by filtering a pulse train through a series of three resonators. This is a simulation of how vowel sounds are made in the vocal tract. In the vocal tract a buzz sound is generated in the larynx and this sound is filtered by the pipe that exists between the larynx and the lips. If we treat the vocal tract as a simple pipe closed at the larynx end and open at the lips, then we can show that such a pipe has a frequency response consisting of a number of simple resonances. In speech science these resonances are called "formants". ESystem simulates the frequency response of a pipe having multiple resonances with a series (cascade) of three simple resonators. ESystem allows you to change the resonant frequencies of the formants but fixes their bandwidths to values typical for a vocal tract. The consequence of passing the input signal through the three resonators in turn is that harmonics of the input signal that are close to any one of the resonant frequencies will be boosted in amplitude, while other harmonics will be attenuated. The output spectrum is made up of harmonics whose fundamental frequency is set by the repetition frequency of the input signal, but whose harmonic amplitudes are influenced by the frequencies of the formants.

Test your understanding

What would we change to alter the pitch of the vowel? We would need to change the fundamental frequency of the input pulse train.

Making vowels of different quality

In this example we will generate a range of vowel qualities.

Choose menu option Input/Pulse Train.
Set the fundamental frequency to 100Hz.
Choose menu option System/Vowel.
Set the formant frequencies to 290, 2600 and 3100Hz.
Listen to the output signal.
Set the formant frequencies to 830, 1560 and 2500Hz.
Listen to the output signal.
Set the formant frequencies to 720, 1060 and 2800Hz.
Listen to the output signal.
Set the formant frequencies to 300, 1100 and 3500Hz.
Listen to the output signal.

The formant frequencies listed here have been taken from a male British English speaker pronouncing the words "heed", "had", "hard" and "who'd". Changes to formant frequencies are caused by changes in the shape of the vocal tract pipe between larynx and lips. These shape changes are caused by movements in the position of the tongue, jaw and lips for the different vowels. However what is important for vowel quality is not the absolute formant frequencies but their relative values. This is because we are used to listening to vowels produced by people with different sized vocal tracts. Smaller vocal tracts will have higher formant frequencies on average than longer vocal tracts.

Test your understanding
Children have smaller vocal tracts than adults so will have higher formant frequencies. In what other way are the vowels of children different?	Children also have smaller larynxes which vibrate more rapidly. Thus a smaller larynx generates an excitation signal with a higher fundamental frequency, which gives vowels which sound higher in pitch.

Making the vowels sound more natural

In this example we will change the input waveform into something that more closely approximates the noise generated by the larynx.

Choose menu option System/Vowel.
Set the formant frequencies to 720, 1060 and 2800Hz.
Choose menu option Input/Sawtooth.
Set the fundamental frequency to 100Hz.
Listen to the input signal and the output signal.
Choose menu option Input/From File ..
Choose the "fallpitch.wav" audio file (distributed with ESystem).
Listen to the input signal and the output signal.

In this example we substitute the pulse train from the previous examples with a sawtooth waveform. The sawtooth has relatively more low-frequency energy than the pulse train, and produces a vowel with significantly more bass. If the vowel sounds a little muffled compared to a natural vowel, it is because of the lack of higher formants in the vowel simulation. The "fallpitch" audio file consists of a sawtooth waveform that changes in fundamental frequency from 130Hz to 90Hz over one second. When played through the vowel filter, this gives a vowel with a much more natural quality. In comparison to an input waveform with a constant fundamental frequency, which tends to have a mechanical quality, an input with changing fundamental is much more like a typical human vowel production.

Test your understanding
Why does the spectrum of "fallpitch.wav" not show clear harmonics?	Because the signal is changing in fundamental frequency, and so the harmonics are not at a constant frequency over the duration of the signal.

5. Introduction to Digital Systems

This is a more advanced topic and may safely be skipped.

Building an amplifier
In this example we will build our own digital system that implements an amplifier.
- Choose menu option Input/Sinewave.
- Set the fundamental frequency to 1000Hz.
- Choose menu option System/User Designed.
- Set the x[n] coefficient to 2, and set all the other coefficients to 0.
- Study the change in amplitude of the signal.
We have built a user designed system with this formula:
y[n] = 2 * x[n]
The convention we will use is that x[] represents the input signal and y[] represents the output signal. The term x[n] represents the n^th input sample, and y[n] represents the n^th output sample. It is understood that this formula is applied for every output sample from n=1 to n=N (N = number of samples in output waveform). Thus you should be able to read the formula as saying that the n^th output sample is twice as large as the n^th input sample. In other words we have built a system that operates as an amplifier with a linear factor of 2, or approximately 6dB.

Test your understanding

How would we build an attenuator that reduced the size of the input signal by a factor of 10 (or −20dB)? Set the coefficient x[n] to 0.1.

Building a simple low-pass filter

In this example we will build our own digital system that implements a kind of low-pass filter.

Choose menu option Input/White noise.
Choose menu option System/User Designed.
Set the x[n] coefficient to 0.5, set the x[n−1] coefficient to 0.5, and set all the other coefficients to 0.
Listen to the input signal and the output signal.
Study the frequency response of the system.

We have built a user designed system with this formula:

y[n] = 0.5 * x[n] + 0.5 * x[n-1]

This system calculates the current output sample from the average of the current input sample and the previous input sample. By x[n−1] we mean the value of the n-1^th input sample. Because this system averages over two samples, this means that any sinewave that has a period close to two samples long will be averaged to a small value. In Esystem, the sampling rate is 12800 samples/second. A sinewave with period equal to two samples will thus have a frequency of 6400Hz. You should see that this system has a dip in its frequency response close to 6400Hz. The system is rather crude low-pass filter.

Test your understanding
If we averaged over three samples (set three coefficient to 0.333), at what frequency would we see the dip in the frequency response?	At 4266Hz, that is 12800/3. Averaging over three samples ensures that any sinewave with a period of three sample averages to zero.

Building a simple high-pass filter
In this example we will build our own digital system that implements a kind of high-pass filter.
- Choose menu option Input/Sawtooth.
- Set the frequency to 100Hz.
- Choose menu option System/User Designed.
- Set the x[n] coefficient to 1.0, set the x[n−1] coefficient to −1.0, and set all the other coefficients to 0.
- Listen to the input signal and the output signal.
- Study the frequency response of the system.
We have built a user designed system with this formula:
y[n] = x[n] − x[n-1]
This system calculates the current output sample from the difference between the current input sample and the previous input sample. This is the same as differentiating the input signal. The consequence is that any constant value shared by the two samples is removed. You can see this clearly in the processing of the sawtooth waveform, where the slowly changing region of the waveform is eliminated. The frequency response graph also shows how the lowest frequency components of a signal are attenuated by differentiation.

Test your understanding

What does a differentiated sinewave look like? Differentiating a sinewave changes its amplitude and its phase but not its shape or frequency.

Building a simple resonator

In this example we will build our own digital system that implements a simple resonator.

Choose menu option Input/Sawtooth.
Set the frequency to 100Hz.
Choose menu option System/User Designed.
Set the x[n] coefficient to 1.0, and set all the other x[] coefficients to 0. Set the coefficient y[n−1] to 1.72, and coefficient y[n−2] to −0.95.
Listen to the input signal and the output signal.
Study the frequency response of the system.

We have built a user designed system with this formula:

y[n] = x[n] + 1.72 * y[n-1] - 0.95 * y[n-2]

This system calculates the current output sample by combining the current input sample with the previous output sample and the output sample before that. This system is different to the earlier examples in that the calculation is recursive, i.e. that the calculation of the nth output sample involves previously calculated values in the output waveform. Recursive systems are considerably more powerful than non-recursive systems. In particular they can create systems with indefinitely long impulse responses. The impulse response of a non-recursive system is limited in length to the number of coefficients used in the definition of the system. One danger though, is that recursive systems can be unstable, where the output waveform gets larger and larger without limit.

The coefficients for generating a simple resonator can be calculated from the resonant frequency and bandwidth according to this recipe:

Step	Example
Set F=Resonant frequency	F=1000
Set B=Bandwidth	B=100
Set S=Sample Rate	S=12800
Set r=1-π*B/S	r=1-3.14159*100/12800=0.975
Set W=2πF/S	W=23.141591000/12800=0.490
Set y[n-1] coeff=2rcos(W) cos() in radians.	y[n-1]=20.975cos(0.490)=1.72
Set y[n-2] coeff=-r*r	y[n-2]=−0.975*0.975=−0.95

Test your understanding
Calculate the y[n−1] and y[n−2] coefficients for a resonator with resonant frequency of 3200Hz and bandwidth 128Hz for ESystem's sampling rate of 12800Hz.	r=1-3.14159128/12800=0.97 W=23.141593200/12800=1.571 y[n-1]=20.97cos(1.571)=0 y[n-2]=-0.970.97=−0.94

Introduction to Convolution

In this example we will demonstrate the arithmetic of convolution that drives the operation of digital systems.

Choose menu option Input/From File.
Choose the input file "3pulses.wav" (supplied with ESystem).
Choose menu option System/User Designed.
Set the x[n] coefficient to 4.0, the x[n−1] coefficient to −2, the x[n−2] coefficient to 2, and the x[n−3] coefficient to −1. Set all the y[] coefficients to 0.
Choose menu option View/Impulse Response
Study the input signal, impulse response and output signal.

We have built a user designed system with this formula:

y[n] = 4 * x[n] - 2 * x[n-1] + 2 * x[n-2] - x[n-3]

The input signal consists of the sample sequence:

0, 1, 2, -2, 0, 0, 0, 0, 0

This example is so small we can actually calculate the output samples values. The way we can do this is to treat the input signal as if it consisted as a stream of pulses of a size equal to the signal amplitude at the sampling instants. In other words instead of the graph ESystem draws, with a smooth line joining points, we pretend the signal only has amplitude at the instants: 1, 2, and 3 seconds. At these we imagine pulses of size 1, 2 and −2.

To calculate the output signal, given the input signal and the impulse response, all we do now is cause each pulse in the input signal to trigger a scaled impulse response. So the pulse at time 1 triggers an inpulse response of size 1, the pulse at time 2 triggers an inpulse response of size 2, and the pulse a time 3 triggers an inpulse response of size −2.

This table shows what happens:


Input	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	4	−2	2	−1	0	0	0
2	0	8	−4	4	−2	0	0
−2	0	0	−8	4	−4	2	0
0	0	0	0	0	0	0	0
Output	4	6	−10	7	−6	2	0

In this table, each input sample triggers a scaled impulse response starting at the time of that sample. For example, the sample at time 3 triggers an impulse response scaled by −2 that starts at time 3. The final output then, is just a sum over all the triggered impulse responses. At time 2 for example, we sum the second value of the impulse response scaled by 1 and the first value of the impulse response scaled by 2.

This process of adding a number of scaled and delayed impulse responses across a single time is called convolution. We can express convolution mathematically as follows:

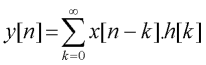
Here h[] represents the system impulse response, which is just the sequence 4,-2,2,-1,0,0,0,... This equation captures the idea that the value of the n^th output sample y[n] is the sum of the first sample of the impulse response scaled by x[n] added to the second sample of the impulse response scaled by x[n−1] added to the third sample of the inpulse response scaled by x[n−2], and so on.

Test your understanding
Why is the "infinity" symbol in the convolution sum not a problem in practice?	Because we can always treat systems as having an impulse response of finite length. Or in other words that past some length all values of h[] are zero. We need only sum over the non-zero values of h[].

Want to learn more?

Books

Signals and Systems for Speech and Hearing (Stuart Rosen, Peter Howell, 1990). This text is a thorough introduction to the concepts of signals and systems analysis that play a role in the speech and hearing sciences, using only minimal mathematics. Written in an informal yet informative style, it provides a comprehensive course for the student and also an excellent reference guide for the specialist. [Academic Press London, ISBN: 0125972318]. Available at Amazon.com and Amazon.co.uk.

Signals and Systems: Models and Behaviour (M.L. Meade, C.R. Dillon, 1991). This book was written for first and second year undergraduates in electronic engineering and the physical sciences with the aim of providing a firm grounding in the study of signals and systems. In this second edition the authors provide a more detailed treatment of the z-transform. A new chapter serves to review and integrate much of the earlier material, while introducing the discrete Fourier transform in the context of signal capture and spectral analysis. These changes reflect the growing important of discrete-time topics in undergraduate studies and the fact that many students now have direct experience in the use and application of signal-processing software. Emphasis is placed on discussion rather than on detailed mathematical proofs, with the aim of developing and encouraging a critical approach to the use of software tools. [Kluwer Academic Publishers; ISBN: 041240110X]. Available at Amazon.com and Amazon.co.uk.

Introductory Digital Signal Processing with Computer Applications (P.A. Lynn, W. Fuerst, B. Thomas, 1997). An essential component of the advanced undergraduate syllabus, digital signal processing continues to be of vital importance in many areas, including communications, radar, sonar, seismology, biomedicine, aeronautics and data analysis. This revised edition gives a practical account of the subject - identifying the main problems and pitfalls of DSP, and detailing how to interpret the results of signal processing. Throughout the text, computer programs are employed to illustrate the fundamental concepts of DSP and to facilitate the practical design of digital filters and processors. For this revised version, all computer programs have been translated into C to increase the appeal to a wider range of users. The disk included with this text provides a graphic display of the results of processing signals and allows the reader to take an interactive role by experimenting with programs. [John Wiley and Sons, ISBN: 0471976318]. Available at Amazon.com and Amazon.co.uk.

On the Web

If you find the study of speech interesting and would like to know more, why not visit the Internet Institute of Speech and Hearing at www.speechandhearing.net ? There you will find tutorials, reference material, laboratory experiments and contact details of professional organisations.

Bug reports

Please send suggestions for improvements and reports of program faults to sfs@pals.ucl.ac.uk.

Please note that we are unable to provide help with the use of this program.

Copyright

ESystem is not public domain software, its intellectual property is owned by Mark Huckvale, University College London. However ESystem may be used and copied without charge as long as the program and help file remain unmodified and continue to carry this copyright notice. Please contact the author for other licensing arrangements. ESystem carries no warranty of any kind, you use it at your own risk.

_{Version 1.1 July 2003}

SFS/ESystemSignals & Systems Tutorial

by Mark Huckvale

1. Basic Operation

2. The Spectrum

3. Systems

4. Generating Vowel-like sounds

5. Introduction to Digital Systems

Want to learn more?

Books

On the Web

Bug reports

Copyright

SFS/ESystem
Signals & Systems Tutorial